2010年高级中等学校招生全国统一考试数学卷(广东深圳)
把分式方程 ,的两边同时乘以x-2,约去分母,得( )
,的两边同时乘以x-2,约去分母,得( )
A 1-(1-x)="1 " B 1+(1-x)="1 " c 1-(1-x)="x-2 " D 1+(1-x)=x-2
小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等。设小明打字速度为x个/分钟,则列方程正确的是( )
A.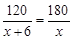 |
B.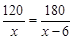 |
C.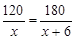 |
D.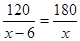 |
下列说法中正确的是( )
A.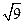 是一个无理数 是一个无理数 |
B.函数y=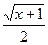 的自变量的取值范围是x﹥-1 的自变量的取值范围是x﹥-1 |
| C.若点P(2,a)和点Q(b,-3)关于x轴对称,则a-b的值为-1 |
| D.-8的立方根是2 |
如图,根据要求回答下列问题:
(1)点A关于y轴对称点A'的坐标是____________;
点B关于y轴对称点B'的坐标是______________;
点C关于y轴对称点C'的坐标是______________;
(2)作出与△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
为保护水资源,某社区新建了雨水再生工程,再生水利用量达58600立方米/年。这个数据用科学记数法表示为(保留两个有效数字)
| A.58×103 | B.5.8×104 | C.5.9×104 | D.6.0×104 |
下列运算正确的是
| A.(x-y)2=x2-y2 | B.x2·y2 =(xy)4 | C.x2y+xy2 =x3y3 | D.x6÷y2 =x4 |
下列说法正确的是
| A.“打开电视机,正在播世界杯足球赛”是必然事件 |
| B.“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就有1次正面朝上 |
| C.一组数据2,3,4,5,5,6的众数和中位数都是5 |
| D.甲组数据的方差S甲2=0.24,乙组数据的方差S甲2=0.03,则乙组数据比甲组数据稳定 |
已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)

观察下列算式,用你所发现的规律得出22010的末位数字是
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,
| A.2 | B.4 | C.6 | D.8 |
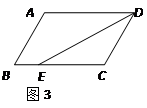
如图1,△ABC中,AC=AD=BD,∠DAC=80º,则∠B的度数是

| A.40º | B.35º | C.25º | D.20º |
有四张质地相同的卡片,它们的背面相同,其中两张的正面印有“粽子”的图案,另外两张的正面印有“龙舟”的图案,现将它们背面朝上,洗均匀后排列在桌面,任意翻开两张,那么两张图案一样的概率是
A. B. C. D.
某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个。设B型包装箱每个可以装x件文具,根据题意列方程为
A.=+12 B.=-12
C.=-12 D.=+12
如图2,点P(3a,a)是反比例函y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为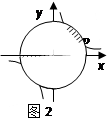
| A.y= | B.y= | C.y= | D.y= |
如图4,是一个由若干个相同的小正方体组成的几何体的主视图和俯视图,则能组成这个几何体的小正方体的个数最少是____________个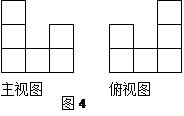
如图5,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60º方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30º方向上,那么该船继续航行____________分钟可使渔船到达离灯塔距离最近的位置.
低碳发展是今年深圳市政府工作报告提出的发展理念.近期,某区与某技术支持单位合作,组织策划了该区“低碳先锋行动”,开展低碳测量和排行活动.根据调查数据制作了频数分布直方图和扇形统计图,图6中从左到右各长方形的高度之比为2:8:9:7:3:1.
(1)已知碳排放值5≤x<7(千克/平方米·月)的单位有16个,则此次行动调查__个单位;
(2)在图7中,碳排放值5≤x<7(千克/平方米·月)部分的圆心角为________度;
(3)小明把图6中碳排放值1≤x<2的都看成1.5,碳排放值2≤x<3的都看成2.5,以此类推,若每个被检单位的建筑面积均为10000平方米,则按小明的办法,可估算碳排放值x≥4(千克/平方米·月)的被检单位一个月的碳排放总值约为________________吨.
如图8,△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90º,D在AB上.

(1)求证:△AOB≌△COD;
(2)若AD=1,BD=2,求CD的长.
儿童商场购进一批M型服装,销售时标价为75元/件,按8折销售仍可获利50%.商场现决定对M型服装开展促销活动,每件在8折的基础上再降价x元销售,已知每天销售数量y(件)与降价x元之间的函数关系为y=20+4x(x>0)
(1)求M型服装的进价;
(2)求促销期间每天销售M型服装所获得的利润W的最大值.销售,已知每天销售数量与降价
如图9,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P坐标.

 中,分式的个数是( )
中,分式的个数是( ) 的图像上的是( )
的图像上的是( ) 的图象位于( )
的图象位于( ) , 0)
, 0) 为反比例函数,则m= ( )
为反比例函数,则m= ( )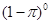 =
= 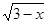 自变量x取值范围是
自变量x取值范围是 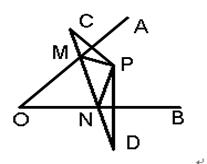


 , 其中x=
, 其中x=

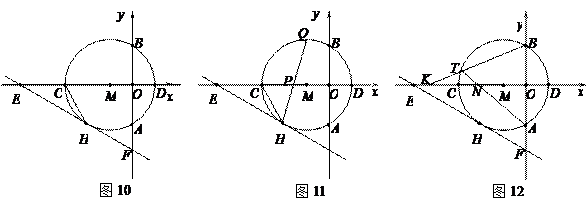
 粤公网安备 44130202000953号
粤公网安备 44130202000953号