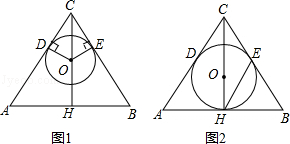
如图10,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙M相切于点H,交x轴于点E,交y轴于点F.
(1)请直接写出OE、⊙M的半径r、CH的长;
(2)如图11,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;
(3)如图12,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
相关知识点
推荐套卷
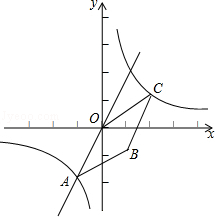
 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.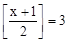 ,求满足条件的所有正整数x.
,求满足条件的所有正整数x.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号