如图所示,点A坐标为(0,3),OA半径为1,点B在x轴上.
⑴若点B坐标为(4,0),⊙B半径为3,试判断⊙A与⊙B位置关系;
⑵若⊙B过M(-2,0)且与⊙A相切,求B点坐标.
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被这个圆所覆盖.例如,图中的三角形被一个圆所覆盖. 回答问题:
边长为1cm的正方形被一个半径为r的圆所覆盖, r的最小值是多少?
边长为1cm的正三角形被一个半径为r的圆所覆盖, r的最小值是多少?
半径为1cm的圆被边长为a的正方形所覆盖, a的最小值是多少?
半径为1cm的圆被边长为a的正三角形所覆盖, a的最小值是多少?
请你类比一条直线和一个圆的三种位置关系,在图①、②、③中,分别各画出一条直线,使它与两个圆都相离、都相切、都相交,并在图④中也画上一条直线,使它与两个圆具有不同于前面3种情况的位置关系.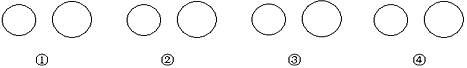
如图, 的直径
的直径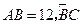 的长为2
的长为2 ,
,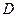 在
在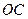 的延长线上,且
的延长线上,且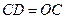 .
.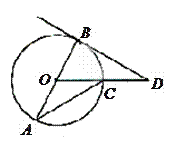
(1)求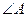 的度数;
的度数;
(2)求证: 是
是 的切线;
的切线;
(参考公式:弧长公式 ,其中
,其中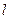 是弧长,
是弧长, 是半径,
是半径,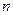 是圆心角度数)
是圆心角度数)
(10分) 如图9,已知,在△ABC中,∠ABC= ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
(1)求证:ED是⊙O的切线.
(2)如果CF ="1,CP" =2,sinA = ,求⊙O的直径BC.
,求⊙O的直径BC.
如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD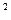 =AB·AE,求证:DE是⊙O的切线.
=AB·AE,求证:DE是⊙O的切线.

第20题图
(本小题满分9分)
如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
(本题满分10分,每小题5分)
请你把上面的解答再认真地检查一遍,别留下什么遗憾,并估算一下成绩是否达到了80分,如果你的全卷得分低于80分,则本题的得分将计入全卷总分,但计入后全卷总分最多不超过80分;如果你全卷得分已经达到或超过80分,则本题的得分不计入全卷总分.
(1)计算 -2 +3的结果是_ _;
(2)如图,点C在⊙O上,∠ACB=50°,则∠AOB=_ _°
(本题满分10分,每小题5分)
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
 为
为 的直径,
的直径, 为弦,且
为弦,且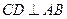 ,垂足为
,垂足为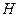 .
.
(1)如果 的半径为4,
的半径为4,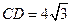 ,求
,求 的度数;
的度数;
(2)若点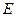 为
为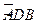 的中点,连结
的中点,连结 ,
, .求证:
.求证: 平分
平分 ;
;
(3)在(1)的条件下,圆周上到直线 距离为3的点有多少个?并说明理由.
距离为3的点有多少个?并说明理由.
如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=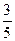 ,求EF的长.
,求EF的长.
如图,AB是8O的直径,点C在BA的延长线上,直线CD与
8O相切于点D,弦DF^AB于点E,线段CD=10,连接BD;

(1) 求证:ÐCDE=2ÐB;
(2) 若BD:AB=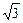 :2,求8O的半径及DF的长。
:2,求8O的半径及DF的长。
如图,已知在⊙O中,AB=4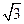 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
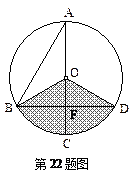
(1)求图中阴影部分的面积;
|
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
如图,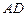 为
为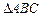 外接圆的直径,
外接圆的直径,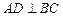 ,垂足为点
,垂足为点 ,
, 的平分线交
的平分线交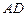 于点
于点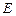 ,连接
,连接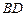 ,
,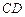 .
.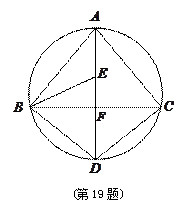
(1) 求证: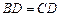 ;
;
(2) 请判断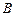 ,
,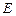 ,
, 三点是否在以
三点是否在以 为圆心,以
为圆心,以 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.
如图,在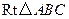 中,
中,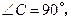 点
点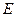 在斜边
在斜边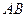 上,以
上,以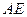 为直径的
为直径的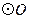 与
与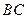 相切于点
相切于点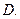

(1)求证: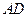 平分
平分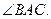
(2)若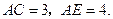 ①求
①求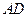 的值;②求图中阴影部分的面积.
的值;②求图中阴影部分的面积.