2010年高级中等学校招生全国统一考试数学卷(辽宁沈阳)
绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
| 穗长 |
4.5≤x<5 |
5≤x<5.5 |
5.5≤x<6 |
6≤x<6.5 |
6.5≤x<7 |
7≤x<7.5 |
| 频数 |
4 |
8 |
12 |
13 |
10 |
3 |
(1)在图1、图2中分别出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.
图1 图2
如图,已知正比例函数y = ax(a≠0)的图象与反比例函致 (k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(1)写出反比例函数和正比例函数的解析式;
(2)试计算△COE的面积是△ODE面积的多少倍.
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200 m、
120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
如图,△ABC内接于⊙O,且∠B = 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
(1)求证:△ACF≌△ACG;
(2)若AF = 4 ,求图中阴影部分的面积.
,求图中阴影部分的面积.
如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于
(A)30° (B)40° (C)60° (D)70°
德州市2009年实现生产总值(GDP)1545.35亿元,用科学记数法表示应是(结果保留3个有效数字)
A. 元 元 |
B. 元 元 |
C. 元 元 |
D. 元 元 |
某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h与注水时间t关系的是
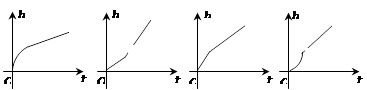
(A) (B) (C) (D)
为了了解某校九年级学生的体能情况,随机抽查了其中50名学生,测试1分钟仰卧起坐的成绩(次数),进行整理后绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,以下同),
请根据统计图计算成绩在20~30次的频率是
| A.0.4 | B.0.5 | C.0.6 | D.0.7 |
已知三角形的三边长分别为3,4,5,则它的边与半径为1的圆的公共点个数所有可能的情况是
| A.0,1,2,3 | B.0,1,2,4 | C.0,1,2,3,4 | D.0,1,2,4,5 |
袋子中装有3个红球和5个白球,这些球除颜色外均相同.在看不到球的条件下,随机从袋中摸出一个球,则摸出白球的概率是_____________.
在四边形 中,点E,F,G,H分别是边AB,BC,CD,DA的中点,如果四边形EFGH为菱形,那么四边形ABCD是 (只要写出一种即可).
中,点E,F,G,H分别是边AB,BC,CD,DA的中点,如果四边形EFGH为菱形,那么四边形ABCD是 (只要写出一种即可).
电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.
如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1= CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2= AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3= BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2009与点P2010之间的距离为_________.
粉笔是校园中最常见的必备品.
图1是一盒刚打开的六角形粉笔,总支数为50支.图2是它的横截面(矩形ABCD),已知每支粉笔的直径为12mm,由此估算矩形ABCD的周长约为_______ mm.( ,结果精确到1 mm)
,结果精确到1 mm)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
| 甲 |
95 |
82 |
88 |
81 |
93 |
79 |
84 |
78 |
| 乙 |
83 |
92 |
80 |
95 |
90 |
80 |
85 |
75 |
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
如图,在△ABC中,AB=AC,D是BC中点,AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A、E两点, 交AD于点G,交AB于点F.
(1)求证:BC与⊙O相切;
(2)当∠BAC=120°时,求∠EFG的度数.
为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若市政府投资140万元,最多能购买多少个太阳能路灯?
为了响应国家“发展低碳经济、走进低碳生活”的号召,到目前为止沈阳市共有60000户家庭建立了“低碳节能减排家庭档案”,则60000这个数用科学记数法表示为
| A.60´104 | B.6´105 | C.6´104 | D.0.6´106 。 |
下列运算正确的是
| A.x2+x3="x5" | B.x8¸x2="x4" | C.3x-2x="1" | D.(x2)3=x6 |
下列事件为必然事件的是
| A.某射击运动员射击一次,命中靶心 | B.任意买一张电影票,座位号是偶数 | C.从一个只有红球的袋子里面摸出一个球是红球 | D.掷一枚质地均匀的硬币落地后正面朝上 。 |
如图,在方格纸上建立的平面直角坐标系中,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△FEC,则点A的对应点F的坐标是
| A.(-1,1) | B.(-1,2) | C.(1,2) | D.(2,1) |
反比例函数y= - 的图像在
的图像在
| A.第一、二象限 | B.第二、三象限 | C.第一、三象限 | D.第二、四象限 |
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且ÐADE=60°,BD=3,CE=2,则△ABC的边长为

| A.9 | B.12 | C.15 | D.18 |
如图,在□ ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 。
在平面直角坐标系中,点A1(1,1),A2(2,4),A3(3,9),A4(4,16),…,用你发现的规律确定点A9的坐标为 。
若等腰梯形ABCD的上、下底之和为2,并且两条对角线所成的锐角为60°,则等腰梯形ABCD的面积为 。
小吴在放假期间去上海参观世博会,小吴根据游客流量,决定第一天从中国馆 (A)、日本馆 (B)、西班牙馆 (C)中随机选一个馆参观,第二天从 法国馆 (D)、沙特馆 (E)、芬兰馆 (F) 中随机选一个馆参观。请你用列表法或画树形图 (树形图)法,求小吴恰好第一天参观 中国馆(A)且第二天参观芬兰馆(F)的概率。(各国家馆可用对应的字母表示)
如图,菱形 的对角线 与 相交于点 ,点 、 分别为边 、 的中点,连接 、 、 .求证:四边形 是菱形.
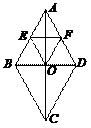
2010年4月14日,国内成品油价格迎来今年的首次提价,某市93号汽油的价格由6.25
元/升涨到了6.52元/升。某报纸调查员就“关于汽油涨价对用车会造成的影响”这一问题向有机动车的私家车车主进行了问卷调查,并制作了统计图表的一部分如下:
| 车主的态度 |
百分比 |
||||
|
m |
||||
| E. 不关心这个问题 |
10% |

(1) 结合上述统计图表可得:p=" " ,m=" " ;
(2) 根据以上信息,请直接在答题卡中补全条形统计图;
(3) 2010年4月末,若该市有机动车的私家车车主约200000人,根据上述信息,请你估计一下持有“影响不大,还可以接受”这种态度的车主约有多少人?
如图,AB是8O的直径,点C在BA的延长线上,直线CD与
8O相切于点D,弦DF^AB于点E,线段CD=10,连接BD;

(1) 求证:ÐCDE=2ÐB;
(2) 若BD:AB=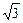 :2,求8O的半径及DF的长。
:2,求8O的半径及DF的长。
阅读下列材料,并解决后面的问题:
★阅读材料:
(1) 等高线概念:在地图上,我们把地面上海拔高度相同的点连成的闭合曲线叫等高线。
例如,如图1,把海拔高度是50米、100米、150米的点分别连接起来,就分别形成50米、100米、150米三条等高线。
(2) 利用等高线地形图求坡度的步骤如下:(如图2)
步骤一:根据两点A、B所在的等高线地形图,分别读出点A、B的高度;A、B两点
的铅直距离=点A、B的高度差;
步骤二:量出AB在等高线地形图上的距离为d个单位,若等高线地形图的比例尺为
1:n,则A、B两点的水平距离=dn;
步骤三:AB的坡度= =
= ;
;

★请按照下列求解过程完成填空,并把所得结果直接写在答题卡上。
某中学学生小明和小丁生活在山城,如图3(示意图),小明每天上学从家A经过B沿着公路AB、BP到学校P,小丁每天上学从家C沿着公路CP到学校P。该山城等高线地形图的比例尺为1:50000,在等高线地形图上量得AB=1.8厘米,BP=3.6厘米,CP=4.2厘米。
(1) 分别求出AB、BP、CP的坡度(同一段路中间坡度的微小变化忽略不计);
(2) 若他们早晨7点同时步行从家出发,中途不停留,谁先到学校?(假设当坡度在 到
到 之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在
之间时,小明和小丁步行的平均速度均约为1.3米/秒;当坡度在 到
到 之间时,小明和小丁步行的平均速度均约为1米/秒)
之间时,小明和小丁步行的平均速度均约为1米/秒)
解:(1) AB的水平距离=1.8´50000=90000(厘米)=900(米),AB的坡度= =
= ;
;
BP的水平距离=3.6´50000=180000(厘米)=1800(米),BP的坡度= =
= ;
;
CP的水平距离=4.2´50000=210000(厘米)=2100(米),CP的坡度=" " j ;
(2) 因为 <
< <
< ,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。 因为 k ,所以小丁在路段CP上步行的平均速度约为 l 米/秒,斜坡 AB的距离=
,所以小明在路段AB、BP上步行的平均速度均约为1.3米/秒。 因为 k ,所以小丁在路段CP上步行的平均速度约为 l 米/秒,斜坡 AB的距离= »906(米),斜坡BP的距离=
»906(米),斜坡BP的距离= »1811(米),斜 坡CP的距离=
»1811(米),斜 坡CP的距离= »2121(米),所以小明从家到学校的时间=
»2121(米),所以小明从家到学校的时间= =2090(秒)。
=2090(秒)。
小丁从家到学校的时间约为 m 秒。因此, n 先到学校。
某公司有甲、乙两个绿色农产品种植基地,在收获期这两个基地当天收获的某种农产品, 一部份存入仓库,另一部分运往外地销售。根据经验,该农产品在收获过程中两个种植基地累积总产量y (吨)与收获天数x (天)满足函数关系y=2x+3 (1£x£10且x为整数)。该农产品在收获过程中甲、乙两基地的累积产量分别占两基地累积总产量的百分比和甲、乙两基地累积存入仓库的量分别占甲、乙两基地的累积产量的百分比如下表:
 项目 项目 |
该基地的累积产量占 两基地累积总产量的百分比 |
该基地累积存入仓库的量占 该基地的累积产量的百分比 |
 百分比 百分比 |
||
| 种植基地 |
||
| 甲 |
60% |
85% |
| 乙 |
40% |
22.5% |
(1) 请用含y的代数式分别表示在收获过程中甲、乙两个基地累积存入仓库的量;
(2) 设在收获过程中甲、乙两基地累积存入仓库的该种农产品的总量为p(吨),请求出p(吨)与收获天数x(天)的函数关系式;
(3) 在(2)基础上,若仓库内原有该农产品42.6吨,为满足本地市场需求,在此收获期开始 的同时,每天从仓库调出一部分该种农产品投入本地市场,若在本地市场售出的该种农产品总量m(吨)与收获天数x(天)满足函数关系m= -x2+13.2x-1.6 (1£x£10且x为整数)。
问在此收获期内连续销售几天,该农产品库存量达到最低值?最低库存量是多少吨?
如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧, BM^直线a于点M,CN^直线a于点N,连接PM、PN;
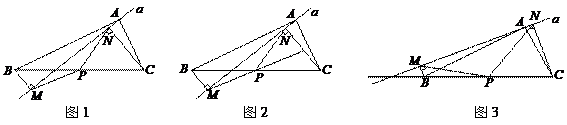 (1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
(1) 延长MP交CN于点E(如图2)。j求证:△BPM@△CPE;k求证:PM = PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。
如图1,在平面直角坐标系中,拋物线y=ax2+c与x轴正半轴交于点F(16,0)、与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合;
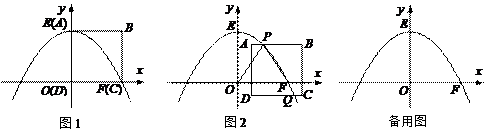
(1) 求拋物线的函数表达式;
(2) 如图2,若正方形ABCD在平面内运动,并且边BC所在的直线始终与x轴垂直,抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时,点P不与A、B两点重合,点Q不与C、D两点重合)。设点A的坐标为(m,n) (m>0)。
j当PO=PF时,分别求出点P和点Q的坐标;
k在j的基础上,当正方形ABCD左右平移时,请直接写出m的取值范围;
l当n=7时,是否存在m的值使点P为AB边中点。若存在,请求出m的值;若不存在,请说明理由。






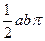
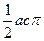
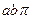
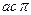
 的解集为_____________.
的解集为_____________. 的解为
的解为 =___________.
=___________. ,其中
,其中 .
.
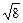 ´
´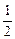 -(
-(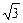 )0=" " 。
)0=" " 。 的解集是 。
的解集是 。 +
+ ,其中x= -1。
,其中x= -1。 粤公网安备 44130202000953号
粤公网安备 44130202000953号