如图，抛物线y = ax2 + bx + 4与x轴的两个交点分别为A（－4，0）、B（2，0），与y轴交于点C，顶点为D．E（1，2）为线段BC的中点，BC的垂直平分线与x轴、y轴分别交于F、G．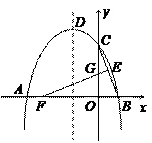
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）在直线EF上求一点H，使△CDH的周长最小，并求出最小周长；
（3）若点K在x轴上方的抛物线上运动，当K运动到什么位置时，
△EFK的面积最大？并求出最大面积．
相关试题
经过（0,-1）,（3,2）两点．求它的解析式及顶点坐标．
和△
中,
,
为线段
上一点,且
．
．
．已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨．某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：
（1）1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？
（2）请你帮该物流公司设计租车方案；
（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱的租车方案，并求出最少租车费．
相关知识点
推荐套卷
粤公网安备 44130202000953号