2010年高级中等学校招生全国统一考试数学卷(山东济宁)
有数颗等重的糖果和数个大、小砝码,其中大砝码皆为5克、大砝码皆为1克,且图(三)是将糖果与砝码放在等臂天平上的两种情形。判断下列哪一种情形是正确的?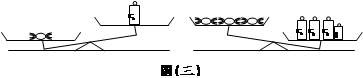

下列四个选项中的数列,哪一个不是等差数列?
A. , , , , , , , , |
B.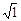 , , , , , ,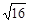 , ,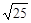 |
C. ,2 ,2 ,3 ,3 ,4 ,4 ,5 ,5 |
D.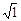 ,2 ,2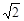 ,3 ,3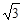 ,4 ,4 ,5 ,5 |
坐标平面上有一函数y=24x2-48的图形,其顶点坐标为何?
| A.(0,-2) | B.(1,-24) | C.(0,-48) | D.(2,48) |
图(四)为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与 交于另一点D。若A=70,B=60,则
交于另一点D。若A=70,B=60,则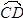 的度数为何?
的度数为何?
| A.50 | B.60 | C.100 | D.120 |
以下有甲、乙、丙、丁四组资料
甲:13,15,11,12,15,11,15 乙:6,9,8,7,9,9,8,5,4
丙:5,4,5,7,1,7,8,7,4 丁:17,11,10,9,5,4,4,3
判断哪一组资料的全距最小?
| A.甲 | B.乙 | C.丙 | D.丁 |
坐标半面上,在第二象限内有一点P,且P点到x轴的距离是4,到y轴的距离是5,则P点坐标为何?
| A.(-5,4) | B.(-4,5) | C.(4,5) | D.(5,-4) |
已知有一多项式与(2x2+5x-2)的和为(2x2+5x+4),求此多项式为何?
| A.2 | B.6 | C.10x+6 | D.4x2+10x+2 |
图(五)数在线的A、B、C三点所表示的数分别为a、b、c。根据图中各点位置,判断下列各式何者正确? 
| A.(a-1)(b-1)>0 | B.(b-1)(c-1)>0 | C.(a+1)(b+1)<0 | D.(b+1)(c+1)<0 |
自连续正整数10~99中选出一个数,其中每个数被选出的机会相等。
求选出的数其十位数字与个位数字的和为9的机率为何?
A.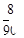 |
B.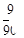 |
C.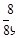 |
D.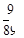 |
将图(六)的正方形色纸沿其中一条对角线对折后,再沿原正方形的另一条对角线对折,如图(七)所示。最后将图(七)的色纸剪下一纸片,如图(八)所示。若下列有一图形为图(八)的展开图,则此图为何?
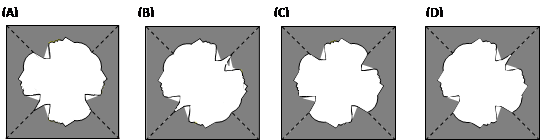
已知456456=23´a´7´11´13´b,其中a、b均为质数。若b>a,则b-a之值为何?
| A.12 | B.14 | C.16 | D.18 |
图(九)为甲、乙两班某次数学成绩的盒状图。若甲、乙两班数学成绩的四分位距分别为a、b;最大数(值)分别为c、d,则a、b、c、d的大小关系,下列何者正确?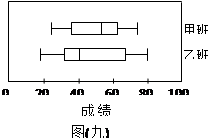
| A.a<b且c<d | B.a<b且c>d | C.a>b且c<d | D.a>b且c>d |
图(十)为一个平行四边形ABCD,其中H、G两点分别在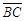 、
、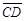 上,
上, ^
^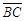 ,
, ^
^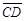 ,且
,且 、
、 、
、 将ÐBAD分成 Ð1、Ð2、Ð3、Ð4四个角。若
将ÐBAD分成 Ð1、Ð2、Ð3、Ð4四个角。若 =5,
=5, =6,则下列关系何者正确?
=6,则下列关系何者正确?

| A.Ð1=Ð2 | B.Ð3=Ð4 | C.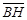 = = |
D.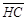 = =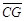 |
已知有大、小两种纸杯与甲、乙两桶果汁,其中小纸杯与大纸杯的容量比为2:3,甲桶果汁与乙桶果汁的体积比为4:5,若甲桶 内的果汁刚好装满小纸杯120个,则乙桶内的果汁最多可装满几个大纸杯?
| A.64 | B.100 | C.144 | D.225 |
如图(十一),△ABC中,有一点P在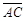 上移动。若
上移动。若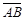 =
=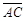 =5,
=5,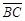 =6,则
=6,则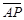 +
+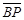 +
+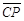 的最小值为何?
的最小值为何?
| A.8 | B.8.8 | C.9.8 | D.10 |
若a为方程式(x-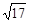 )2=100的一根,b为方程式(y-4)2=17的一根,且a、b都是正数,则a-b之值为何?
)2=100的一根,b为方程式(y-4)2=17的一根,且a、b都是正数,则a-b之值为何?
| A.5 | B.6 | C.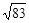 |
D.10-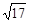 |
坐标平面上,若移动二次函数y=2(x-175)(x-176)+6的图形,使其与x轴交于两点,且此两点的距离为1单位,则移动方式可为下列哪一种?
| A.向上移动3单位 | B.向下移动3单位 | C.向上移勤6单位 | D.向下移动6单位 |
如图(十二),直线CP是 的中垂线且交
的中垂线且交 于P,其中
于P,其中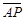 =2
=2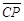 。甲、乙两人想在
。甲、乙两人想在 上取两点D、E,使得
上取两点D、E,使得 =
=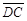 =
=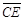 =
= ,其作法如下:
,其作法如下:

(甲) 作ÐACP、ÐBCP之角平分线,分别交 于D、E,则D、E即为所求
于D、E,则D、E即为所求
(乙) 作 、
、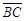 之中垂线,分别交
之中垂线,分别交 于D、E,则D、E即为所求对于甲、乙两人的作法,下列判断何者正确?
于D、E,则D、E即为所求对于甲、乙两人的作法,下列判断何者正确?
| A.两人都正确 | B.两人都错误 | C.甲正确,乙错误 | D.甲错误,乙正确 |
如图(十三),扇形AOB中, =10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在
=10, ÐAOB=36°。若固定B点,将此扇形依顺时针方向旋转,得一新扇形A’O’B,其中A点在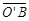 上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
上,如图(十四)所示,则O点旋转至O’点所经过的轨迹长度为何?
甲、乙两种机器分利以固定速率生产一批货物,若4台甲机器和2台乙机器同时运转3小时的总产量,与2台甲机器和5台乙机器同时运转2小时的总产量相同,则1台甲机器运转1小时的产量,与1台乙机器运转几小时的产量相同?
A.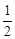 |
B.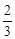 |
C.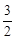 |
D.2 |
据统计部门报告,我市去年国民生产总值为238 770 000 000元, 那么这个数据用科学记数法表示为
| A.2. 3877×10 12元 | B.2. 3877×10 11元 |
| C.2 3877×10 7元 | D.2387. 7×10 8元 |
若一个三角形三个内角度数的比为2︰3︰4,那么这个三角形是
| A.直角三角形 | B.锐角三角形 | C.钝角三角形 | D.等边三角形 |
已知⊙O1与⊙O2相切,⊙O1的半径为3 cm,⊙O2的半径为2 cm,则O1O2的长是
| A.1 cm | B.5 cm | C.1 cm或5 cm | D.0.5cm或2.5cm |
如图,是张老师出门散步时离家的距离 与时间
与时间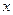 之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是
之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是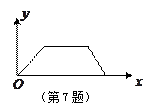
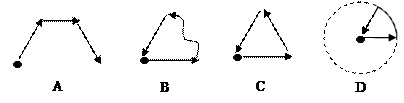
如图,是有几个相同的小正方体搭成的几何体的三种视图, 则搭成这个几何体的小正方体的个数是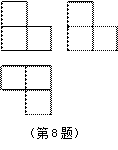
| A.3个 | B.4个 | C.5个 | D.6个 |
如图,如果从半径为9cm的圆形纸片剪去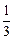 圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为
| A.6cm | B.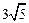 cm cm |
C.8cm | D.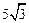 cm cm |
在一次夏令营活动中,小霞同学从营地 点出发,要到距离
点出发,要到距离 点
点
 的
的 地去,先沿北偏东
地去,先沿北偏东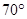 方向到达
方向到达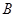 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了
 到达目的地
到达目的地 ,此时小霞在营地
,此时小霞在营地 的
的
A.北偏东 方向上 方向上 |
B.北偏东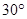 方向上 方向上 |
C.北偏东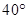 方向上 方向上 |
D.北偏西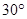 方向上 方向上 |
如图,是一张宽 的矩形台球桌
的矩形台球桌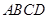 ,一球从点
,一球从点 (点
(点 在长边
在长边 上)
上)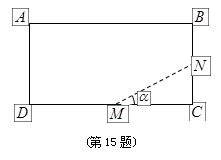
出发沿虚线 射向边
射向边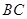 ,然后反弹到边
,然后反弹到边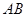 上的
上的 点. 如果
点. 如果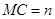 ,
,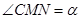 .那么
.那么 点与
点与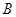 点的距离为 .
点的距离为 .
上海世博会自2010年5月1日到10月31日,历时184天.预测参观人数达7000万人次.如图是此次盛会在5月中旬入园人数的统计情况.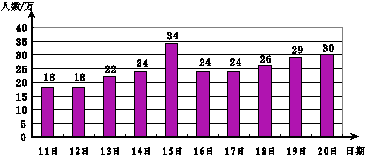
(1)请根据统计图完成下表.
| |
众数 |
中位数 |
极差 |
| 入园人数/万 |
|
|
|
(2)推算世博会期间参观总人数与预测人数相差多少?
观察下面的变形规律: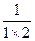 =1-
=1- ;
; 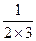 =
= -
-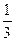 ;
; =
=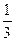 -
- ;……
;……
解答下面的问题:
(1)若n为正整数,请你猜想 = ;
= ;
(2)证明你猜想的结论;
(3)求和: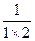 +
+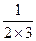 +
+ +…+
+…+ .
.
如图,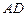 为
为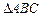 外接圆的直径,
外接圆的直径,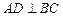 ,垂足为点
,垂足为点 ,
, 的平分线交
的平分线交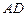 于点
于点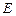 ,连接
,连接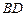 ,
, .
.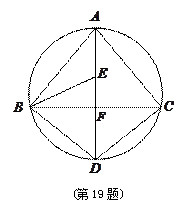
(1) 求证: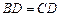 ;
;
(2) 请判断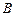 ,
,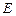 ,
, 三点是否在以
三点是否在以 为圆心,以
为圆心,以 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.
如图,正比例函数 的图象与反比例函数
的图象与反比例函数
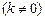 在第一象限的图象交于
在第一象限的图象交于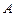 点,过
点,过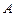 点作
点作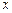 轴的垂线,垂足为
轴的垂线,垂足为 ,已知
,已知 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果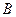 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点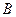 与点
与点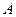 不重合),且
不重合),且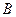 点的横坐标为1,在
点的横坐标为1,在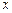 轴上求一点
轴上求一点 ,使
,使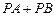 最小.
最小.
某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
数学课上,李老师出示了这样一道题目:如图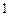 ,正方形
,正方形 的边长为
的边长为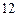 ,
,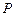 为边
为边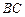 延长线上的一点,
延长线上的一点,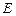 为
为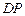 的中点,
的中点,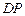 的垂直平分线交边
的垂直平分线交边 于
于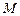 ,交边
,交边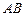 的延长线于
的延长线于 .当
.当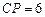 时,
时,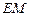 与
与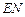 的比值是多少?
的比值是多少?
经过思考,小明展示了一种正确的解题思路:过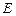 作直线平行于
作直线平行于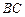 交
交 ,
,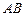 分别于
分别于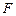 ,
,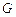 ,如图
,如图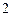 ,则可得:
,则可得: ,因为
,因为 ,所以
,所以 .可求出
.可求出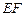 和
和 的值,进而可求得
的值,进而可求得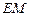 与
与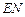 的比值.
的比值.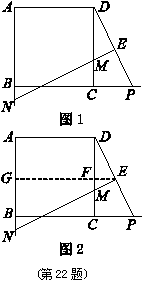
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究,得出了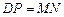 的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.
如图,在平面直角坐标系中,顶点为(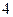 ,
,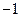 )的抛物线交
)的抛物线交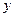 轴于
轴于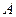 点,交
点,交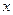 轴于
轴于 ,
,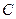 两点(点
两点(点 在点
在点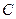 的左侧). 已知
的左侧). 已知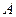 点坐标为(
点坐标为(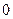 ,
,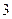 ).
).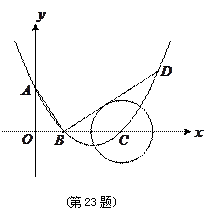
(1)求此抛物线的解析式;
(2)过点 作线段
作线段 的垂线交抛物线于点
的垂线交抛物线于点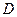 , 如果以点
, 如果以点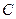 为圆心的圆与直线
为圆心的圆与直线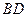 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴 与⊙
与⊙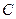 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于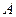 ,
,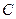 两点之间,问:当点
两点之间,问:当点
如图1,在平面直角坐标系中,拋物线y=ax2+c与x轴正半轴交于点F(16,0)、与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合;
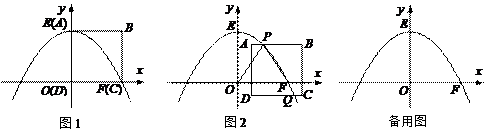
(1) 求拋物线的函数表达式;
(2) 如图2,若正方形ABCD在平面内运动,并且边BC所在的直线始终与x轴垂直,抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时,点P不与A、B两点重合,点Q不与C、D两点重合)。设点A的坐标为(m,n) (m>0)。
j当PO=PF时,分别求出点P和点Q的坐标;
k在j的基础上,当正方形ABCD左右平移时,请直接写出m的取值范围;
l当n=7时,是否存在m的值使点P为AB边中点。若存在,请求出m的值;若不存在,请说明理由。
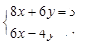 ,得y=?
,得y=?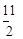
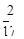
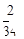
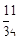
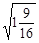 +
+ 之值为何?
之值为何?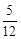
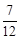
 分解因式,结果正确的是
分解因式,结果正确的是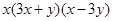
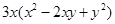
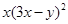

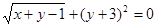 ,则
,则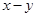 的值为
的值为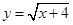 中, 自变量
中, 自变量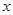 的取值范围是 .
的取值范围是 .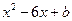 可化为
可化为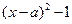 ,则
,则 的值是 .
的值是 .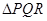 是
是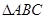 经过某种变换后得到的图形.
经过某种变换后得到的图形.
 的坐标为(
的坐标为(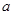 ,
, ),它的对应点
),它的对应点 的坐标为 .
的坐标为 .
 粤公网安备 44130202000953号
粤公网安备 44130202000953号