初中数学圆幂定理试题

如图，在△ABC中，分别以AB，AC为直径在△ABC外作半圆和半圆，其中和分别为两个半圆的圆心. F是边BC的中点，点D和点E分别为两个半圆圆弧的中点.

（1）连结，
证明：；
（2）如图，过点A分别作半圆和半圆的切线，交BD的延长线和CE的延长线于点P和点Q，连结PQ，若∠ACB=90°,DB=5，CE=3，求线段PQ的长;

（3）如图三，过点A作半圆的切线，交CE的延长线于点Q，过点Q作直线FA的垂线，交BD的延长线于点P，连结PA. 证明：PA是半圆的切线.

如图，AB是的直径，AC是弦，直线EF和相切与点C，，垂足为D.

（1）求证；
（2）如图，若把直线EF向上移动，使得EF与相交于G，C两点（点C在点G的右侧），连结
AC，AG，若题中其他条件不变，这时图中是否存在与相等的角？若存在，找出一个这样
的角，并证明；若不存在，说明理由.

如图，E，B，A，F四点共线，点D是正三角形ABC的边AC的中点，点是直线上异于A，B的一个动点，且满足，则                                           （   ）

A．点一定在射线上

B．点一定在线段上

C．点可以在射线上，也可以在线段上

D．点可以在射线上，也可以在线段上

如图，第一象限内半径为2的⊙C与y轴相切于点A，作直径AD，过点D作⊙C的切线l交x轴子点B，P为直线l上一动点，已知直线PA的解析式为：y＝kx＋3。
(1)设点P的纵坐标为p，写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M，与AB交于点N，则不论动点P处于直线l上（除点B以外）的什么位置时，都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明；
(3)是否存在使△AMN的面积等于的k值？若存在，请求出符合的k值；若不存在，请说明理由。

如图，在直角坐标系xOy中，点A在x轴的正半轴上，点B在y轴的正半轴上, 以OB为直径的⊙C与AB交于点D， DE与⊙C相切交x轴于点E, 且OA=cm，∠OAB="30°."

（1）求点B的坐标及直线AB的解析式;
（2）过点B作BG^EC于 F, 交x轴于点G, 求BD的长及点F的坐标;
（3）设点P从点A开始沿ABG的方向以4cm/s的速度匀速向点G移动，点Q同时
从点A开始沿AG匀速向点G移动, 当四边形CBPQ为平行四边形时, 求点Q的移动
速度.

如图，在矩形中，，，点从开始沿折线A-B-C-D以4cm/s的速度移动，点从开始沿边以1cm/s的速度移动，如果点、分别从、同时出发，当其中一点到达时，另一点也随之停止运动。设运动时间为t(s)。
⑴t为何值时，四边形为矩形？
⑵如图10-20，如果和的半径都是2cm，那么t为何值时，和外切。

如图，顺次连结圆内接矩形各边的中点，得到菱形ABCD，若BD＝10，DF＝4，则菱形ABCD的边长为(  )

A．4．	B．5
C．6．	D．9．

已知RtABC的两直角边AC、BC分别是一元二次方程的两根，则此Rt的外接圆的面积为              。

如图，BD是⊙O的直径，AB与⊙O相切于点B，过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E．
①试探究AE与⊙O的位置关系，并说明理由；
②已知EC=a，ED=b，AB=c，请你思考后，选用以上适当的数据，设计出计算⊙O的半径r的一种方案；
1) 你选用的已知数是_________；
2) 写出求解过程(结果用字母表示)．

小平所在的学习小组发现，车辆转弯时，能否顺利通过直角弯道的标图2是某巷子的俯视图，巷子路面宽4 m，转弯处为直角，车辆的车身为矩形ABCD，CD与DE、CE的夹角都是45°时，连接EF，交CD于点G，若GF的长度至少能达到车身宽度，即车辆能通过．
（1）小平认为长8m，宽3m的消防车不能通过该直角转弯，请你帮他说明理由；
为半径的弧），长8m，宽3m的消防车就可以通过该弯道了，具体的方案如图3，其中OM⊥OM′，你能帮小平算出，ON至少为多少时，这种消防车可以通过该巷子，？

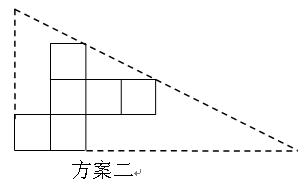
操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：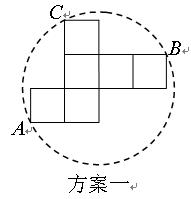
 

纸片利用率=×100%
发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．
探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直
接写出方案三的利用率．

如图，在△ABC中，AB=AC，点O为底边上的中点，以点O为圆心，
1为半径的半圆与边AB相切于点D．
（1）判断直线AC与⊙O的位置关系，并说明理由；
（2）当∠A＝60°时，求图中阴影部分的面积．

（本题满分14分，第（1）题4分，第（2）题4分，第（2）题6分）
在梯形ABCD中，AD//BC，AB⊥AD，AB=4，AD=5，CD=5．E为底边BC上一点，以点E为圆心，BE为半径画⊙E交直线DE于点F．
（1）如图，当点F在线段DE上时，设BE，DF，试建立关于的函数关系式，
并写出自变量的取值范围；
（2）当以CD直径的⊙O与⊙E与相切时，求的值；
（3）联接AF、BF，当△ABF是以AF为腰的等腰三角形时，求的值。

如图（3），在三角板△ABC中，∠ACB = 90℃，∠B = 60℃，BC = 1，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB延长线上时即停止转动，则点A转过的路径长为                  .

D

（11·贵港）
如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．

（1）求证：△AOB∽△BDC；
（2）设大圆的半径为x，CD的长为y：
①求y与x之间的函数关系式；
②当BE与小圆相切时，求x的值．