初中数学圆幂定理填空题

如图，点C，D是半圆O的三等分点，直径AB=．连结AC交半径OD于E，则线段DE，CE以及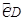围成的封闭图形（即阴影部分）的面积是         ．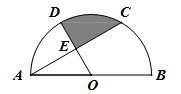

如图，正六边形ABCDEF的边长为2cm，点P为六边形内任一点．则点P到各边距离之和为        cm．

如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为           ．

如图，在扇形AOB中，∠AOB=90°，弧AB的长为2π，则扇形AOB的面积为       ．

如图，已知点A（0，1），B（0，-1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于             度．

在如图所示的平面直角坐标系中，点A（2，9），B（2，3），C（3，2），D（9，2）在⊙P上，则圆心P的坐标是      ．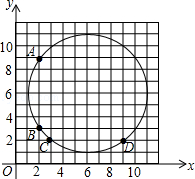

已知△ABC内接于⊙O，过点A作直线EF．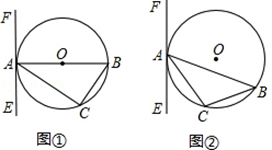

（1）如图①所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）：       或者       ．
（2）如图②所示，如果AB是不过圆心O的弦，且∠CAE=∠B，那么EF是⊙O的切线吗？试证明你的判断．

如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：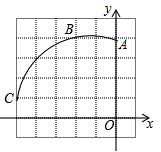

（1）利用网格确定该圆弧所在圆的圆心D点的位置，并写出点D坐标为            ；
（2）连接AD、CD，则⊙D的半径为         （结果保留根号），∠ADC的度数为           ；   
（3）若扇形DAC是一个圆锥的侧面展开图，则该圆锥底面半径为            ．（结果保留根号）．

如图，在平面直角坐标系xOy中，A（-2，0），B（0，2），⊙O的半径为1，点C为⊙O上一动点，过点B作BP⊥直线AC，垂足为点P，则P点纵坐标的最大值为              cm．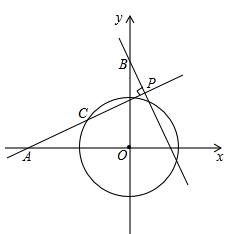
 

如图，正方形ABCD的边长为6，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE=  ________．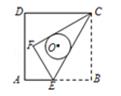

如图，是一个供滑板爱好者使用的U型池，该U型池可以看作是一个长方体去掉一个“半圆柱”而成，中间可供滑行的部分的截面是半径为5m的半圆，其边缘AB=CD=20cm，小明要在AB上选取一点E，能够使他从点D滑到点E再到点C的滑行距离最短，则他滑行的最短距离为         m．（π取3）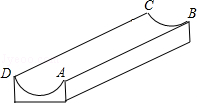

如图，直线y＝x－2与x轴、y轴分别交于M、N两点，现有半径为1的动圆圆心位于原点处，并以每秒1个单位的速度向右作平移运动．已知动圆在移动过程中与直线MN有公共点产生，当第一次出现公共点到最后一次出现公共点，这样一次过程中该动圆一共移动    秒．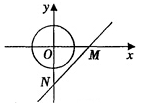

如图，半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N，则劣弧的长度为            ．

如图，⊙I为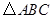的内切圆，点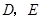分别为边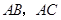上的点，且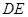为⊙I的切线，若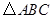的周长为21，边的长为6，则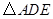的周长为（ ）．

A．15

B．8

C．9

D．7．5

由“不在同一直线上的三点确定一个圆”，可以判断平面直角坐标系内的三个点A（3，0）、B（0，﹣4）、C（2，﹣3）                确定一个圆（填“能”或“不能”）．