江苏省无锡市江阴市马镇九年级上学期12月联考数学试卷
⊙O的半径为5cm,A是线段OP的中点,当OP=7cm时,点A与⊙O的位置关系是( )
| A.点A在⊙O内 | B.点A在⊙O上 |
| C.点A在⊙O外 | D.不能确定 |
对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
| A.开口向下 |
| B.对称轴是x=-1 |
| C.顶点坐标是(1,2) |
| D.与x轴有两个交点 |
餐桌的桌面是长160厘米、宽100厘米的长方形,妈妈准备设计一块桌布,面积是桌面的2倍,且使四周垂下的边等宽.小明设四周垂下的边宽x厘米,则应列方程为( )
A. |
B. |
C. |
D.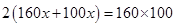 |
如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是( )
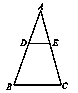
| A.2 | B.3 | C.4 | D.5 |
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
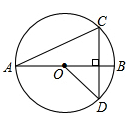
| A.120° | B.140° | C.150° | D.160° |
如图,AC是⊙O的直径,点B, D在⊙O上,那么图中等于∠BOC一半的角有( )
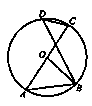
| A.4 个 | B.3 个 | C.2 个 | D.l 个 |
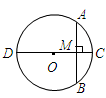
如图,在⊙O中,直径CD=10cm,AB是⊙O的弦,AB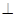 CD,垂足为M,0M:OC=3:5,则AB的长为( )
CD,垂足为M,0M:OC=3:5,则AB的长为( )
| A.8cm | B.6cm | C.2cm | D.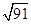 cm cm |
根据下列表格的对应值:请判断方程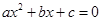 (a≠0,a,b,c为常数)一个解x的范围是( ).
(a≠0,a,b,c为常数)一个解x的范围是( ).
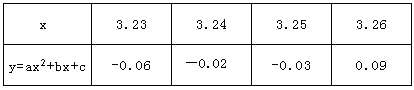
| A.3<x<3.23 | B.3.23<x<3.24 |
| C.3.24<x<3.25 | D.3.25<x<3.26 |
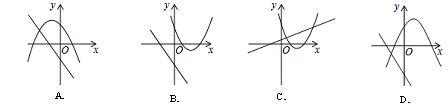
在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数且m≠0)的图象可能是( )
我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4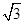 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 ( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是 ( )
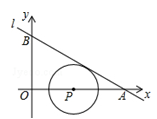
A.6 B.8 C.10 D.12
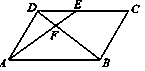
如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=
4:25,则DE:EC= ________.
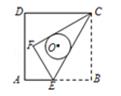
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE= ________.
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为其中正确的有________.(填序号)
如图,在△ABC中,AB=AC= ,BC=2,在BC上有100个不同的点P1、P2、P3…P100(BC中点除外),过这100个点分别作△ABC的内接矩形P1E1F1G1,P2E2F2G2…P100E100F100G100,设每个内接矩形的周长分别为L1、L2…L100,则L1+L2+…+L100=_________.
,BC=2,在BC上有100个不同的点P1、P2、P3…P100(BC中点除外),过这100个点分别作△ABC的内接矩形P1E1F1G1,P2E2F2G2…P100E100F100G100,设每个内接矩形的周长分别为L1、L2…L100,则L1+L2+…+L100=_________.
某校要从九年级(1)班和(2)班中各选取10名女同学组成礼仪队,选取的女生的身高(单位:厘米)如下:
(1)班:168 167 170 165 168 166 171 168 167 170
(2)班:165 167 169 170 165 168 170 171 168 167
(1)补充完整下面的统计分析表;
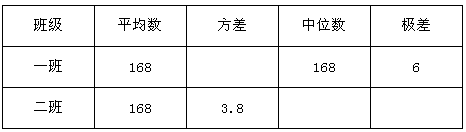
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
一个不透明的布袋里装有红、黄、绿三种颜色的球(除颜色不同,其它均无任何区别),其中红球2个,黄球1个,绿球1个.
(1)求从袋中任意摸出一个球是红球的概率;
(2)第一次从袋中任意摸出一个球,记下颜色后放回袋中,第二次再摸出一个球记下颜色,请用画树状图或列表的方法求两次都摸到红球的概率(两个红球分别记作红1、红2).
如图,点A、B、C分别是⊙O上的点, CD是⊙O的直径,P是CD延长线上的一点,AP=AC.
(1)若∠B=60°,求证:AP是⊙O的切线;
(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE·AB的值.
如图,A(-1,0),B(2,-3)两点都在一次函数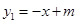 与二次函数
与二次函数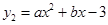 的图象上.
的图象上.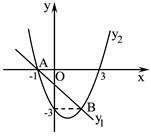
(1)求m和二次函数的解析式;
(2)请直接写出当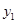 >
>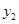 时,自变量
时,自变量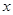 的取值范围.
的取值范围.
(3)说出所求的抛物线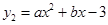 可由抛物线y=x2如何平移得到?
可由抛物线y=x2如何平移得到?
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元,请比较哪种方案的最大利润更高,并说明理由。
阅读理解:如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
(1)如图①,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.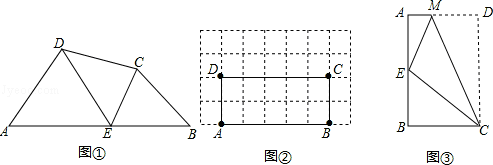
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正△ABC的边长为1,它的一边AC在MN上,且顶点A与M重合.现将正△ABC在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.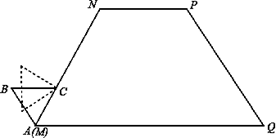
(1)请在所给的图中,画出顶点A在正△ABC整个翻滚过程中所经过的路线图;
(2)求正△ABC在整个翻滚过程中顶点A所经过的路径长;
(3)求正△ABC在整个翻滚过程中顶点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
如图,抛物线y= x2-
x2- x-12与x轴交于A、C两点,与y轴交于B点.
x-12与x轴交于A、C两点,与y轴交于B点.
(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动。问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBAN面积的最大值.
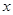 的方程x2-3x+m=0的一个根是1,则另一个根为________.
的方程x2-3x+m=0的一个根是1,则另一个根为________.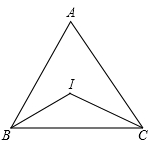

 粤公网安备 44130202000953号
粤公网安备 44130202000953号