2011年初中毕业升学考试(广西贵港卷)数学
如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=____。
将下列长度的三条线段首尾顺次相接,能组成三角形的是( )。
| A.1cm,2 cm,3 cm | B.2 cm,3 cm,5 cm |
| C.5cm,6 cm,10 cm | D.25cm,12 cm,11 cm |
在同一平面内,不重合的两条直线的位置关系是( )。
| A.平行 | B.相交 | C.平行或相交 | D.平行、相交或垂直 |
若用同一种正多边形瓷砖铺地面,能铺满地面的正多边形是( )。
| A.正五边形 | B.正六边形 | C.正七边形 | D.正八边形 |
有下列两个命题:①若两个角是对顶角,则这两个角相等;②若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形。说法正确的是( )。
| A.命题①、②都正确 | B.命题①正确,命题②不正确 |
| C.命题①不正确,命题②正确 | D.命题①、②都不正确 |
如图,DH∥EG∥BC,DC∥EF,那么与∠EFB相等的角(不包括∠EFB)的个
数为( )
A.2个 B.3个 C.4个 D.5个
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D。
试说明:AC∥DF。
解:因为 ∠1=∠2(已知)
∠1=∠3,∠2=∠4( )
所以∠3=∠4(等量代换)
所以 ∥ ( )
所以 ∠C=∠ABD,( )
又因为 ∠C=∠D(已知)
所以∠D=∠ABD(等量代换)
所以 AC∥DF( )
在平面直角坐标系中,顺次连结A(-2,0)、B(4,0)、C(-2,-3)各点,试求:
(1)A、B两点之间的距离。
(2)点C到X轴的距离。
(3)△ABC的面积。
如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,
A点在C处的北偏西45°方向,求∠BAC及∠BCA的度数?
如图,直线CD与直线AB相交于C,根据下列语句画图、解答。
(1)过点P作PQ∥CD,交AB于点Q
(2)过点P作PR⊥CD,垂足为R
(3)若∠DCB=1200,猜想∠PQC是多少度?并说明理由
如图,△ABC中,BD是∠ABC的平分线,DE∥BC交AB于E,∠A=60°,
∠BDC=100°求∠BDE的度数。
某服装销售商在进行市场占有率的调查时,他最应该关注的是……………( )
| A.服装型号的平均数 | B.服装型号的众数 |
| C.服装型号的中位数 | D.最小的服装型号 |
汶川地震后,某电视台法制频道在端午节组织发起“绿丝带行动”,号召市民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是………………………( )
| A.正方形 | B.等腰梯形 |
| C.菱形 | D.矩形 |
(11·贵港)下列说法正确的是
| A.为了了解全国中学生的心理健康情况,应采用全面调查的方式 |
| B.一组数据5,6,7,6,6,8,10的众数和中位数都是6 |
| C.一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 |
| D.若甲组数据的方差S甲2=0.05,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定 |
(11·贵港)若关于x的一元二次方程x2-mx-2=0的一个根为-1,则另一个根为
| A.1 | B.-1 | C.2 | D.-2 |
(11·贵港)如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,
AD=2 ,则tan∠CAD的值是
,则tan∠CAD的值是
| A.2 | B. |
C. |
D. |

(11·贵港)如图所示,在矩形ABCD中,AB= ,BC=2,对角线AC、BD
,BC=2,对角线AC、BD
相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是
A. B.
B. C.1 D.1.5
C.1 D.1.5
(11·贵港)如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD
于点F,AD=4,EF=5,则梯形ABCD的面积是
| A.40 | B.30 | C.20 | D.10 |

(11·贵港)如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标
为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是 _ ▲ .
(11·贵港)从2,3,4,5这四个数字中,任意抽取两个不同数字组成一个两位
数,则这个两位数能被3整除的概率是_ ▲ .
(11·贵港)如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
(11·贵港)如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四
边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于_ ▲ cm2.
(11·贵港)如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中
点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长
交CB的延长线于点G,则BG的长是_ ▲ .
(11·贵港)若记y=f(x)= ,其中f(1)表示当x=1时y的值,即f(1)=
,其中f(1)表示当x=1时y的值,即f(1)=
= ;f(
;f( )表示当x=
)表示当x= 时y的值,即f(
时y的值,即f( )=
)= =
= ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( )+f(3)
)+f(3)
+f( )+…+f(2011)+f(
)+…+f(2011)+f( )=_ ▲ .
)=_ ▲ .
(11·贵港)(本题满分11分,第(1)题5分,第(2)题6分)
(1)(11·贵港)计算:(-1)2011+ -2sin60º+|-1|;
-2sin60º+|-1|;

(11·贵港)如图所示,反比例函数y= 的图象与一次函数y
的图象与一次函数y
=kx-3的图象在第一象限内相交于点A (4,m).
(1)求m的值及一次函数的解析式;
(2)若直线x=2与反比例和一次函数的图象分别交于点B、C,求线段BC的长.
(11·贵港)
按要求用尺规作图(只保留作图痕迹,不必写出作法)
(1)在图(1)中作出∠ABC的平分线;(2)在图(2)中作出△DEF的外接圆O.
(11·贵港)
“校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图:
根据以上图表信息,解答下列问题:
( 1)统计表中的A=_ ▲ ;
1)统计表中的A=_ ▲ ;
(2)统计图中表示 家长“赞成”的圆心角的度数为_ ▲ 度;
家长“赞成”的圆心角的度数为_ ▲ 度;
(3)从这次接受调查的学生中,随机抽查一个,恰好是持“反对”态度的学生的概率是多少?
(11·贵港)
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°, CE=2BE,试判断△CDE的形状,并说明理由.
CE=2BE,试判断△CDE的形状,并说明理由.
(11·贵港)
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭.据某市交通部门统计,2008年底该市汽车拥有量为75万辆,而截止到201 0年底,该市的汽车拥有量已达108万辆.
0年底,该市的汽车拥有量已达108万辆.
(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;
(2)为了保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012
年底全市汽车拥有量不超过125.48万辆;另据统计,从2011年初起,该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同,请你估算出该市从2011
年初起每年新增汽车数量最多不超过多少万辆.
(11·贵港)
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
①求y与x之间的函数关系式;
②当BE与小圆相切时,求x的值.

 中,
中, ,则
,则 的取值范围是 。
的取值范围是 。




 被直线
被直线 所截,
所截, ∥
∥ ,如果
,如果 ,求∠1的度数。
,求∠1的度数。
 中,
中, 是
是 边上的高,
边上的高, 是
是 平分线.
平分线. ,
, 。
。
 的度数;
的度数; 的度数.
的度数.


 经过点(1,-2),则k的值是_ ▲ .
经过点(1,-2),则k的值是_ ▲ .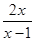 =1的解是x=_ ▲ .
=1的解是x=_ ▲ . x+2与抛物线y=a (x+2) 2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
x+2与抛物线y=a (x+2) 2相交于A、B两点,点A在y轴上,M为抛物线的顶点.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号