（11·贵港）
如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点
A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．
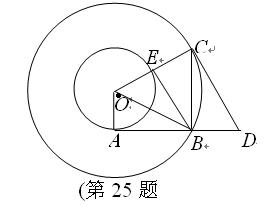
（1）求证：△AOB∽△BDC；
（2）设大圆的半径为x，CD的长为y：
①求y与x之间的函数关系式；
②当BE与小圆相切时，求x的值．
相关知识点
推荐套卷
（11·贵港）
如图所示，在以O为圆心的两个同心圆中，小圆的半径为1，AB与小圆相切于点A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．
（1）求证：△AOB∽△BDC；
（2）设大圆的半径为x，CD的长为y：
①求y与x之间的函数关系式；
②当BE与小圆相切时，求x的值．
粤公网安备 44130202000953号