如图,在矩形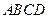 中,
中,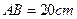 ,
,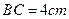 ,点
,点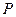 从
从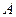 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点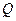 从
从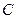 开始沿
开始沿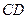 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点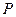 、
、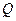 分别从
分别从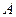 、
、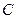 同时出发,当其中一点到达
同时出发,当其中一点到达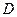 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。
⑴t为何值时,四边形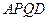 为矩形?
为矩形?
⑵如图10-20,如果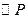 和
和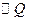 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时,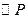 和
和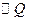 外切。
外切。
相关知识点
推荐套卷
如图,在矩形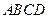 中,
中,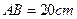 ,
,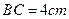 ,点
,点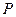 从
从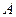 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点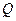 从
从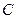 开始沿
开始沿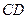 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点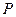 、
、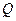 分别从
分别从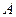 、
、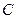 同时出发,当其中一点到达
同时出发,当其中一点到达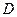 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。
⑴t为何值时,四边形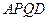 为矩形?
为矩形?
⑵如图10-20,如果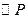 和
和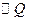 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时,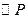 和
和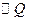 外切。
外切。