如图，第一象限内半径为2的⊙C与y轴相切于点A，作直径AD，过点D作⊙C的切线l交x轴子点B，P为直线l上一动点，已知直线PA的解析式为：y＝kx＋3。
(1)设点P的纵坐标为p，写出p随k变化的函数关系式。
(2)设⊙C与PA交于点M，与AB交于点N，则不论动点P处于直线l上（除点B以外）的什么位置时，都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明；
(3)是否存在使△AMN的面积等于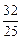
的k值？若存在，请求出符合的k值；若不存在，请说明理由。
相关试题
为了参加全市中学生“党史知识竞赛”，某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛．
（1）如果已经确定女生甲参加，再从其余的候选人中随机选取1人，则女生乙被选中的概率是 ；
（2）求所选代表恰好为1名女生和1名男生的概率．
端午节吃粽子是中华民族的传统习俗．某食品厂为了解市民对去年销量较好的 、 、 、 四种粽子的喜爱情况，在端午节前对某小区居民进行抽样调查（每人只选一种粽子），并将调查情况绘制成两幅尚不完整的统计图．
根据以上信息，解答下列问题：
（1）补全条形统计图；
（2）扇形统计图中， 种粽子所在扇形的圆心角是 ；
（3）这个小区有2500人，请你估计爱吃 种粽子的人数为 ．
相关知识点
推荐套卷
粤公网安备 44130202000953号