如图，已知圆的半径是5，弦AB的长是6，则弦AB的弦心距是（ ）
| A．3 | B．4 | C．5 | D．8 |
如图，AB是半圆O的直径，点P从点O出发，沿线段OA—弧AB—线段OB的路径运动一周．设
为
，运动时间为
，则下列图形能大致地刻画与之间关系的是（ ）
如图，
是
的直径，
是的切线，点
在上，
，
则
的长为（ ）
A． |
B． |
C． |
D． |
如图，⊙Ｏ的半径
弦
点
为弦
上一动点，则点到圆心
的最短距离是 cm． 
如图，以BC为直径的⊙O1与⊙O2外切，⊙O1与⊙O2的外公切线交于点D，且∠ADC=60°，过B点的⊙O1的切线交其中一条外公切线于点A．若⊙O2的面积为π，则四边形ABCD的面积是 ．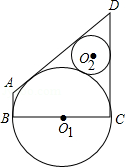
如图，AB是⊙O的直径，AC是弦．
（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；
第一步，过点A作∠BAC的角平分线，交⊙O于点D；
第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．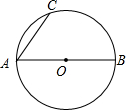
（2）求证：AD2=AE•AB；
（3）连接EO，交AD于点F，若5AC=3AB，求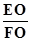
的值．
如图，AB是⊙O的直径，点C在BA的延长线上，直线CD与⊙O相切于点D，弦DF⊥AB于点E，线段CD=10，连接BD
（1）求证：∠CDE=2∠B
（2）若BD：AB=
：2，求⊙O的半径及弦DF的长
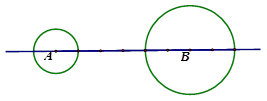
如图８, ⊙A、⊙B的圆心A、B都在直线a上，⊙A的半径为1cm，⊙B的半径为2 cm，圆心距AB＝6cm，现⊙A沿直线a以每秒1cm的速度向右移动，设运动时间为t 秒，那么两圆相切时，t 的取值为 ；
|
第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:接受问卷调查的学生共有___________名；
请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小；
若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到“了解”和“基本了解”程度的总人数.
如图，已知⊙O的直径AB垂直于弦CD,垂足为E，F为CD延长线上一点，AF交⊙O于点G. 求证：AC2=AG·AF
如图，在直角坐标系中，⊙O的圆心O在坐标原点，直径AB=8，点P是直径AB上的一个动点（点P不与A、B两点重合），过点P的直线PQ的解析式为
，当直线PQ交y轴于Q，交⊙O于C、D两点时，过点C作CE垂直于x轴交⊙O于点E，过点E作EG垂直于y轴，垂足为G，过点C作CF垂直于y轴，垂足为F，连接DE．
（1）点P在运动过程中，
∠CPB= ；
（2）当m=3时，试求矩形CEGF的面积；
（3）当P在运动过程中，探索
的值是否会发生变化？如果发生变化，请你说明理由；如果不发生变化，请你求出这个不变的值；
（4）如果点P在射线AB上运动，当△PDE的面积为4时，请你求出CD的长度
如图，AB、ED是⊙O的直径，点C在ED延长线上, 且∠CBD =∠FAB．点F在⊙O上，且 AB⊥DF．连接AD并延长交BC于点G．
求证：BC是⊙O的切线；
求证：BD·BC=BE·CD；
若⊙O 的半径为r，BC=3r，求tan∠CDG的值
如图，矩形ABCD中，AB=6，BC=3．点E在线段BA上从B点以每秒1个单位的速度出发向A点运动，F是射线CD上一动点，在点E、F运动的过程中始终保持EF=5，且CF>BE，点P是EF的中点，连接AP．设点E运动时间为ts.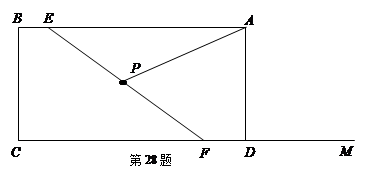
在点E运动过程中，AP的长度是如何变化的？（ ）
| A．一直变短 | B．一直变长 | C．先变长后变短 | D．先变短后变长 |
在点E、F运动的过程中，AP的长度存在一个最小值，当AP的长度取得最小值时，点P的位置应该在 ．
以P为圆心作⊙P，当⊙P与矩形ABCD三边所在直线都相切时，求出此时t的值，并指出此时⊙P的半径长．
如图，在△ABD中，∠A=∠B=30°，以AB边上一点O为圆心，过A，D两点作⊙O交AB于C.
判断直线BD与⊙O的位置关系，并说明理由；
连接CD，若CD=5，求AB的长.
如图，△ABC的3个顶点都在⊙O上，直径AD=2，∠ABC=30°，则AC的长度为
粤公网安备 44130202000953号
