[广西]2012年初中毕业升学考试(广西柳州卷)数学
小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是( )
| A.FG | B.FH | C.EH | D.EF |

如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )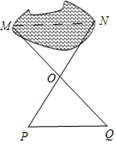
| A.PO | B.PQ | C.MO | D.MQ |
如图,给出了正方形ABCD的面积的四个表达式,其中错误的是( )
| A.(x+a)(x+a) | B.x2+a2+2ax |
| C.(x-a)(x-a) | D.(x+a)a+(x+a)x |
定圆O的半径是4cm,动圆P的半径是2cm,动圆在直线l上移动,当两圆相切时,OP的值是( )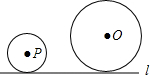
| A.2cm或6cm | B.2cm | C.4cm | D.6cm |
如图,P1、P2、P3这三个点中,在第二象限内的有( )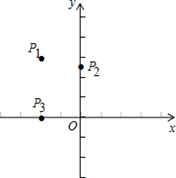
| A.P1、P2、P3 | B.P1、P2 | C.P1、P3 | D.P1 |
如图,小红做了一个实验,将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置,所转过的度数是( )
| A.60° | B.72° | C.108° | D.120° |
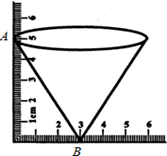
小芳给你一个如图所示的量角器,如果你用它来度量角的度数,那么能精确地读出的最小度数是( )
| A.1° | B.5° | C.10° | D.180° |
小兰画了一个函数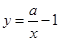 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程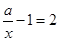 的解是( )
的解是( )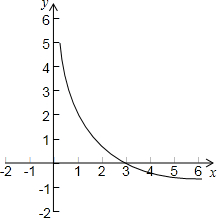
| A.x=1 | B.x="2" | C.x="3" | D.x="4" |
已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为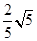 (即cosC=
(即cosC=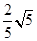 ),则AC边上的中线长是 .
),则AC边上的中线长是 .
列方程解应用题:
今年“六•一”儿童节,张红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?
右表反映了x与y之间存在某种函数关系,现给出了几种可能的函数关系式:
y=x+7,y=x-5,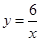 ,
,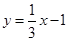
| x |
… |
-6 |
-5 |
3 |
4 |
… |
| y |
… |
1 |
1.2 |
-2 |
-1.5 |
… |
(1)从所给出的几个式子中选出一个你认为满足上表要求的函数表达式: ;
(2)请说明你选择这个函数表达式的理由.
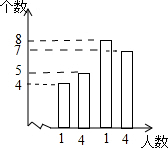
在甲、乙两个袋子中分别装有如图点数的牌,假设随机从袋子中抽牌时,每张牌被抽到的机会是均等的.那么分别从两个袋子各抽取1张牌时,它们的点数之和大于10的概率是多少?
如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个特殊的四边形.
(1)这个特殊的四边形应该叫做 ;
(2)请证明你的结论.
已知:抛物线 .
.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
如图,AB是⊙O的直径,AC是弦.
(1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑);
第一步,过点A作∠BAC的角平分线,交⊙O于点D;
第二步,过点D作AC的垂线,交AC的延长线于点E.
第三步,连接BD.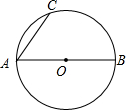
(2)求证:AD2=AE•AB;
(3)连接EO,交AD于点F,若5AC=3AB,求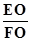 的值.
的值.
如图,在△ABC中,AB=2,AC="BC=" 5 .
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=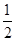 S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).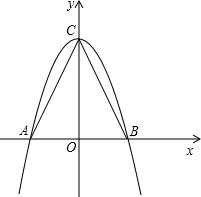
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3=" 3" ,y4="-" 3 .
所以,原方程的解是y1=1,y2=-1,y3=" 3" ,y4="-" 3 .
再如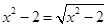 ,可设
,可设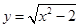 ,用同样的方法也可求解.
,用同样的方法也可求解.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号