[云南]2011届云南省昭通市高中(中专)招生统一模拟考试数学试卷(3)
有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为
| A.8人 | B.9人 | C.10人 | D.11人 |
已知圆锥的底面半径为5cm,侧面积为 cm2,设圆锥的母线与高的夹角为
cm2,设圆锥的母线与高的夹角为 (如图 所示),则
(如图 所示),则 的值为( )
的值为( )
A. |
B. |
C. |
D. |

如图,在直角梯形 中,AB∥CD;
中,AB∥CD; ⊥
⊥ 动点
动点 从点
从点 出发,沿
出发,沿 ,
, 运动至点
运动至点 停止.设点
停止.设点 运动的路程为
运动的路程为 ,
, 的面积为
的面积为 ,如果
,如果 关于
关于 的函数图象如图所示,则
的函数图象如图所示,则 的面积是( )
的面积是( )
| A.3 | B.4 | C.5 | D.6 |

据报道,全球观看广州亚运会开幕式现场直播的观众达16300000000人,该观众人数可用科学记数法表示为____________人.
如图,在菱形ABCD中, ,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则
,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则 ________度.
________度.
下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第 个图中所贴剪纸“○”的个数为
个图中所贴剪纸“○”的个数为 .
.
某区从参加初中八年级数学调研考试的8000名学生成绩中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得到表一;随后汇总整个样本数据,得到表二.
请根据表一、表二所提供的信息,回答下列问题:
(1)样本中,学生数学成绩平均分约为 分(结果精确到0.1);
(2)样本中,数学成绩在84≤x<96分数段的频数为 ,等级为A的人数占抽样学生总数的百分比为 ,中位数所在的分数段为 ;
已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,
轴于点E, .
.
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
为实现区域教育均衡发展,我市计划对某县 、
、 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所 类学校和两所
类学校和两所 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所 类学校和一所
类学校和一所 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所 类学校和一所
类学校和一所 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的 类学校不超过5所,则
类学校不超过5所,则 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县 、
、 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到 、
、 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
在云南大理坐落着美丽的大理三塔.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量三塔中一塔的高度,携带的测量工具有:测角仪.皮尺.小镜子.
(1)小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点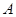 ,用测角仪测出看塔顶
,用测角仪测出看塔顶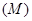 的仰角
的仰角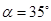 ,在
,在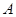 点和塔之间选择一点
点和塔之间选择一点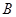 ,测出看塔顶
,测出看塔顶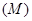 的仰角
的仰角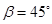 ,然后用皮尺量出
,然后用皮尺量出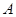 .
.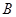 两点的距离为
两点的距离为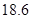 m,自身的高度为
m,自身的高度为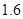 m.请你利用上述数据帮助小华计算出塔的高度(
m.请你利用上述数据帮助小华计算出塔的高度(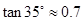 ,结果保留整数).
,结果保留整数).
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影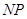 的长为
的长为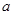 m(如图2),你能否利用这一数据设计一个测量方案?如果能,
m(如图2),你能否利用这一数据设计一个测量方案?如果能,
请回答下列问题:
①在你设计的测量方案中,选用的测量工具是: ;
②要计算出塔的高,你还需要测量哪些数据? .
阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.
数学老师给小明同学出了一道题目:在图正方形网格(每个小正方形边长为1)中画出格点△ABC,使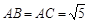 ,
,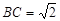 ;
;
小明同学的做法是:由勾股定理,得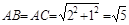 ,
,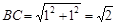 ,于是画出线段AB、AC、BC,从而画出格点△ABC.
,于是画出线段AB、AC、BC,从而画出格点△ABC.
(1)请你参考小明同学的做法,在图中的正方形网格(每个小正方形边长为1)中画出格点△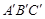 (
(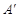 点位置如图所示),使
点位置如图所示),使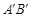 =
=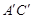 =5,
=5,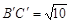 .(直接画出图形,不写过程);
.(直接画出图形,不写过程);
(2)观察△ABC与△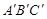 的形状,猜想∠BAC与∠
的形状,猜想∠BAC与∠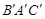 有怎样的数量关系,并证明你的猜想.
有怎样的数量关系,并证明你的猜想. 
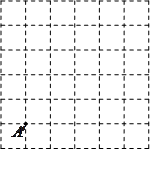
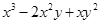 分解因式,结果正确的是( )
分解因式,结果正确的是( )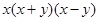
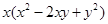
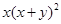







 的图象的顶点坐标是( )
的图象的顶点坐标是( )



 ,若
,若 ,则
,则 的度数是( )
的度数是( )




 在数轴上的位置如图所示,则下列结论正确的是( )
在数轴上的位置如图所示,则下列结论正确的是( )



 =__________.
=__________.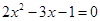 的两根为
的两根为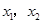 ,则
,则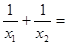 ___________.
___________. 的解集是
的解集是 ,那么
,那么 的值为 .
的值为 . 弦
弦 点
点 为弦
为弦 上一动点,则点
上一动点,则点 的最短距离是 cm.
的最短距离是 cm. 
 与
与 是位似图形,且顶点都在格点上,则位似中心的坐标是 .
是位似图形,且顶点都在格点上,则位似中心的坐标是 .
 .
. ,其中
,其中 .
. 是等边三角形,
是等边三角形,  点是
点是 的中点,延长
的中点,延长 到
到 ,使
,使 ,过
,过 ,垂足是
,垂足是 .求证:
.求证:


 粤公网安备 44130202000953号
粤公网安备 44130202000953号