小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选.
(1)用树状图或列表法求出小明先挑选的概率;
(2)你认为这个游戏公平吗?请说明理由.
相关知识点
推荐套卷

 (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.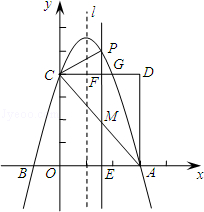

 。
。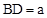 。
。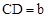 。
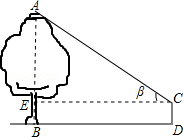
。
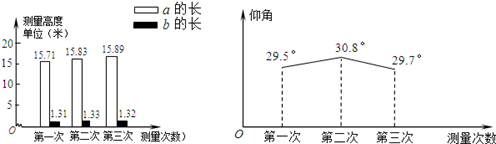



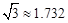 ,
, ,结果保留3个有效数字)。
,结果保留3个有效数字)。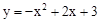 的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。
的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变)。 (
(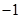 ,3),再向下平移2个单位得到
,3),再向下平移2个单位得到 (
( (0,4),再向下平移2个单位得到
(0,4),再向下平移2个单位得到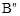 (0,2)。
(0,2)。 。
。 ,解得:
,解得: 。
。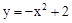 。
。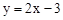 向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。
向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式。 粤公网安备 44130202000953号
粤公网安备 44130202000953号