[江西]2011届江西省中考数学预测试卷六解析版
江西省总面积为16.69万平方千米,约占我国国土面积的 1.7℅, 16.69万平方千米用科学记数法表示为(保留三个有效数字)( )
1.7℅, 16.69万平方千米用科学记数法表示为(保留三个有效数字)( )
| A.7.3×107 | B.7.31×107 | C.7.30×107 | D.7.31×106 |
已知点A(x1,y1)、B(x2,y2)在反比例函数y=- 的图象上,且x1<0<x2,则y1、
的图象上,且x1<0<x2,则y1、
y2和0的大小关系( )
| A.y1>y2>0 | B.y1<y2<0 | C.y1>0>y2 | D.y1<0<y2 |
如图,有一张一个角为 的直角三角形纸片沿其一条中位线剪开后,不能拼成
的直角三角形纸片沿其一条中位线剪开后,不能拼成
的四边形有 ( )
A.邻边不等的矩形  |
B.等腰梯形 |
C.有一角是锐角的菱形  |
D.正方形 |
一个由相同小立方体组成的几何体的俯视图与主视图如图所示,则组成这个几何体的小正方体至少有( )
| A.4个 | B.5个 |
| C.6个 | D.7个 |
如图,一束光线以入射角为 的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成
的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成 的角,则CD与地面AB 所成的角
的角,则CD与地面AB 所成的角 CDA 的度数是
CDA 的度数是 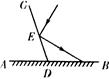
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是 .

如图,半径为5的⊙P与x轴交于点M(0,-4),N(0,-10). 函数y= (x<0)的图
(x<0)的图
象过点P,则下列说法正确的有 .(填序号)
①⊙P与x轴相离; ②△PMN的面积为14;
③⊙P的坐标为(-4,-7); ④k的值为28.
已知一次函数的图象过A(—2,—3),B(1,3)两点。
(1)求这个一次函数的解析式
(2)试判断点P(—1,1)是否在这个一次函数的图象上
有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2。B布袋中有三个完全相同的小球,分别标有数字—1,—2和—3。小明从A布袋中随机抽出一个小球,记录其标有的数字为 ,再从B布袋中随机抽出一个小球,记录其标有的数字为
,再从B布袋中随机抽出一个小球,记录其标有的数字为 。他用这两个数字确定一个点P的坐标为
。他用这两个数字确定一个点P的坐标为
(1)用 列表或画树状图的方法点P的所有可能坐标
列表或画树状图的方法点P的所有可能坐标
(2)求点P落在直线 上的概率
上的概率
某班同学对南昌市市民对于“八一南昌起义”这件事的了解程度进行调查,他们将了解程度分为“清楚”、“了解”、“知道”“不知道”四级将调查结果绘制成以下统计表和条形统计图

(1) 这次调查的样本容量是 
(2)若将四种情况用扇形统计图表示,则“了解”和“知道”两种情况所对圆心角和为
度
(3)补充统计表和条形统计图
(4)若南昌市共有市民480万人,请你估计“清楚”这一事件的可能有多少人?
据研究,当洗衣机中洗衣粉的含量在0.2%~0.5%之间时,衣服的洗涤效果较好,因为这时表面活性较大,现将4.94千克的衣服放入最大容量为15kg的洗衣机中,欲使洗衣机中洗衣粉的含量达到0.4%,那么洗衣机中需要加入多少千克水,多少匙洗衣粉?(1匙洗衣粉约0.02kg,假设洗衣机以最大容量洗涤)
如图,BD是⊙O的直径,AB与⊙O相切于点B,过点D作OA的平行线交⊙O于点C,AC与BD的延长线相交于点E.
①试探究AE与⊙O的位置关系,并说明理由;
②已知EC=a,ED=b,AB=c,请你思考后,选用以上适当的数据,设计出计算⊙O的半径r的一种方案;
1) 你选用的已知数是_________;
2) 写出求解过程(结果用字母表示).
如图所示,电工李师傅借助梯子安装天花板上距地面2.90m的顶灯,已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m,矩形面与地面所成的角α为78°,李师傅的身高为1.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便。
(1)为了安全在梯子的第二段间接一根绳子,绳子最短应是多少?(两边打结处共用绳0.6m)
(2)他现在竖直站立在梯子的第三级踏板上,请你通过计算判断他 安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
安装是否比较方便?(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)
如图,已知抛物线y=x2+bx+c经过A(1,0),B (0,2)两点,顶点为D。
(0,2)两点,顶点为D。
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B,顶点为D,若点N 在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标。
在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标。
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在 斜边AB的中点P处,
斜边AB的中点P处, 将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点,如图3-1-13①②③是旋转三角板得到的图形中的3种情况,
将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点,如图3-1-13①②③是旋转三角板得到的图形中的3种情况,
由①②③研究:(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图①加以证明。
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由)。
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图④加以证明。



 的相反数是( )
的相反数是( )
 +
+ 的结果为( )
的结果为( ) 的解集是( )
的解集是( ) —
— (
( —
— 的结果是()
的结果是() 3
3 C
C  后,输出的结果应为
后,输出的结果应为  tan60°的值为
tan60°的值为 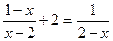
 粤公网安备 44130202000953号
粤公网安备 44130202000953号