初中数学一次函数的最值解答题

已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数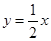的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．

已知一次函数y=kx+b的图像经过点（－1．－5），且与正比例函数y=x的图象相交于点（2，m）．
（1）求m的值；
（2）求一次函数y=kx+b的解析式；
（3）求这两个函数图像与x轴所围成的三角形面积．

某公司有A型产品40件，B型产品60件，分配给下属甲、乙两个商店销售，其中70件给甲店，30件给乙店，且都能卖完，两商店销售这两种产品每件的利润（元）如下表：

	A型利润	B型利润
甲店	200	170
乙店	160	150

 
（1）设分配给甲店A型产品x件，这件公司卖出这100件产品的总利润W（元），求W关于x的函数关系式，并求出x的取值范围；
（2）若要求总利润不低于17560元，有多少种不同分配方案，并将各种方案设计出来；
（3）为了促销，公司决定仅对甲店A型产品让利销售，每件让利a元，但让利后A型产品的每件利润仍高于甲店B型产品的每件利润．甲店的B型产品以及乙店的A、B型产品的每件利润不变，问该公司又如何设计分配方案，使总利润达到最大．

如图，已知一次函数与反比例函数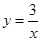的图象交于A，B两点．求A，B两点的坐标．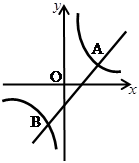

瓦甸科星化工有限公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时 ，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式，并写出自变量x的取值范围
（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？ 

已知一次函数y=kx+b图象过点（0，2），且与两坐标轴围成的三角形面积为2，求此一次函数的解析式．

某学校要印制一批《学生手册》，甲印刷厂提出：每本收1元印刷费，另收500元制版费；乙印刷厂提出：每本收2元印刷费，不收制版费．
（1）分别写出甲、乙两厂的收费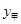 （元）、（元）与印制数量x（本）之间的关系式；
（2）问：该学校选择哪间印刷厂印制《学生手册》比较合算？请说明理由．

如图，直线的函数关系式为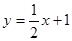，且与x轴交于点D，直线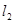经过定点A（4，0），B（-1，5），直线与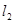相交于点C，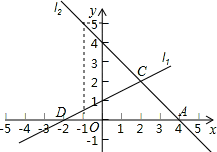

（1）求直线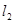的解析式；
（2）求△ADC的面积；
（3）在直线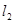上存在一点F（不与C重合），使得△ADF和△ADC的面积相等，请求出F点的坐标；
（4）在x轴上是否存在一点E，使得△BCE的周长最短，若存在请求出E点的坐标，若不存在，请说明理由．

已知甲、乙两地相距300km，小轿车从甲地出发驶往乙地，同时货车从相距乙地60km的入口A处驶往甲地（两车均在甲、乙两地之间的公路上匀速行驶），如图是它们离甲地的路程y（km）与货车行驶时间x（h）之间的函数的部分图像．

（1）求货车离甲地的路程y（km）与它行驶的时间x（h）的函数表达式；
（2）哪一辆车先到达目的地（小轿车达到乙地；货车到达甲地）？说明理由．

小明从兴化通过申通快递公司给在南京的朋友寄一盒苹果，快递时，他了解到申通快递公司除了收取每次6元的包装费外，苹果不超过2kg时收费22元，若超过2kg，则超过的部分按每千克10元收取费用，该公司从兴化到南京快递苹果的费用为y（元），小明所寄的苹果为x（kg）（x＞2）
（1）求y与x的函数关系式；
（2）已知小明给朋友寄了2．5kg的苹果，请你求出这次快递的费用．

用图像法求二元一次方程组的解．

已知y与x-3成正比例，当x=4时，y=3；
（1）求y与x的函数式；
（2）当x=2时，求y的值．

为了响应政府提出的由中国制造向中国创造转型的号召，某公司自主设计了一款成本为40元的可控温杯，并投放市场进行试销售，经过调查发现该产品每天的销售量y（件）与销售单价x（元）满足一次函数关系：y=﹣10x+1200．
（1）求利润S（元）与销售单价x（元）之间的关系式；
（2）当销售单价定为多少时，该公司每天获取的利润最大？最大利润是多少元？

如图①，△OAB中，A（0，2），B（4，0），将△AOB向右平移m个单位，得到△O′A′B′．
（1）当m=4时，如图②．若反比例函数y =的图象经过点A′，一次函数y=ax+b的图象经过A′、B′两点．求反比例函数及一次函数的表达式；
（2）若反比例函数y=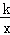的图象经过点A′及A′B′的中点M，求m的值．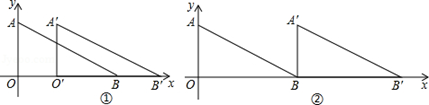

在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如图所示．
 
（1）试判断y与x之间的函数关系，并求出函数关系式．
（2）若许愿瓶的进价为6元/个，按照上述市场调查销售规律，求利润w（元）与销售单价x（元/个）之间的函数关系式．
（3）若许愿瓶的进货成本不超过900元，要想获得最大利润，试求此时这种许愿瓶的销售单价，并求出最大利润．