“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．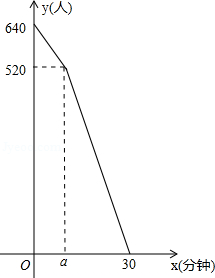
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？
某市政府为了增强城镇居民抵御大病风险的能力，积极完善城镇居民医疗保险制度，纳入医疗保险的居民的大病住院医疗费用的报销比例标准如下表：
| 医疗费用范围 |
报销比例标准 |
| 不超过8000元 |
不予报销 |
| 超过8000元且不超过30000元的部分 |
50% |
| 超过30000元且不超过50000元的部分 |
60% |
| 超过50000元的部分 |
70% |
设享受医保的某居民一年的大病住院医疗费用为x元，按上述标准报销的金额为y元．
（1）直接写出x≤50000时，y关于x的函数关系式，并注明自变量x的取值范围；
（2）若某居民大病住院医疗费用按标准报销了20000元，问他住院医疗费用是多少元？
已知一次函数y=kx+b的图象经过点（﹣1，﹣5），且与正比例函数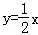
的图象相交于点（2，m）．
求：（1）m的值；
（2）一次函数y=kx+b的解析式；
（3）这两个函数图象与x轴所围成的三角形面积．
某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表．
| |
A种产品 |
B种产品 |
| 成本（万元/件） |
2 |
5 |
| 利润（万元/件） |
1 |
3 |
（1）若工厂计划投入资金不多于44万元，且获利多于14万元，问工厂有几种生产方案？
（2）在（1）的条件下，如何生产能使获利最大？并求出最大利润．
你一定知道乌鸦喝水的故事吧！一个紧口瓶中盛有一些水，乌鸦想喝，但是嘴够不着瓶中的水，于是乌鸦衔来一些小石子放入瓶中，瓶中水面的高度随石子的增多而上升，乌鸦喝到了水．但是还没解渴，瓶中水面就下降到乌鸦够不着的高度，乌鸦只好再去衔些石子放入瓶中，水面又上升，乌鸦终于喝足了水，哇哇地飞走了．如果设衔入瓶中石子的体积为x，瓶中水面的高度为Y，下面能大致表示上面故事情节的图象是（ ）
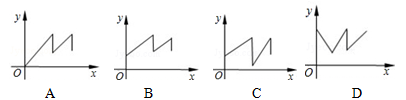
如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）
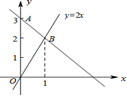
| A．y=2x+3 | B．y=x﹣3 | C．y=2x﹣3 | D．y=﹣x+3 |
如图，直线y=k（x-2）+k-1与x轴、y轴分别交于B、C两点，且
．
（1）求B点坐标和k值；
（2）若点A（x，y）是直线y=k（x-2）+k-1（k>0）上在第一象限内的一个动点，
①当点A在运动过程中，试写出△AOB的面积S与x的函数关系式；（不要求写出自变量的取值范围）
②当A点运动到什么位置时，△AOB的面积为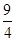
，并说明理由；
③在②成立的情况下，x轴上是否存在一点P，使△AOP是等腰三角形？若存在，请直接写出满足条件的所有P点坐标；若不存在，请说明理由．
“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．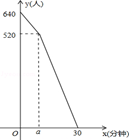
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？
如图，直角坐标系中，点P（t，0）是x轴上的一个动点，过点P作y轴的平行线，分别与直线y=
x，直线y=﹣x交于A，B两点，以AB为边向右侧作正方形ABCD．
（1）当t=2时，正方形ABCD的周长是 ．
（2）当点（2，0）在正方形ABCD内部时（不包括边上），t的取值范围是 ．
粤公网安备 44130202000953号
+2是一次函数，那么m的值是（ ）
与平均每天使用的小时数
之间的函数关系式为 ．
和
的图象相交于点A（
，3），则不等式
的解集为 ．