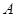初中数学一次函数的最值解答题

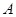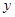        、两座城市之间有一条高速公路，甲、乙两辆汽车同时分别从这条路两端的入口处驶入，并始终在高速公路上正常行驶．甲车驶往城，乙车驶往城，甲车在行驶过程中速度始终不变．甲车距城高速公路入口处的距离（千米）与行驶时间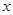（时）之间的关系如图．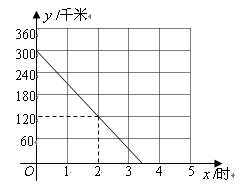

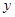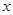（1）求关于的表达式；
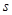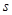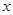（2）已知乙车以60千米/时的速度匀速行驶，设行驶过程中，相遇前两车相距的路程为（千米）．请直接写出关于的表达式；
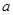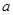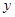（3）当乙车按（2）中的状态行驶与甲车相遇后，速度随即改为（千米/时）并保持匀速行驶，结果比甲车晚40分钟到达终点，求乙车变化后的速度．在下图中画出乙车离开城高速公路入口处的距离（千米）与行驶时间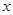（时）之间的函数图象．

．(本题8分) 已知，关于x的一次函数的图像不经过第三象限．
（1）当时，  ▲ y  ▲ ．（用含a的代数式表示）
（2）确定a的取值范围．

如图，四边形A1OC1B1、A2C1C2B2、A3C2C3B3均为正方形，点A₁、A₂、A₃和点C₁、C₂、C₃分别在直线y=x+1和x轴上，求点C₁和点B₃的坐标.

有甲、乙两个均装有进水管和出水管的容器，水管的所有阀门都处于关闭状态．初始时，同时打开甲、乙两容器的进水管，两容器都只进水；到8分钟时，关闭甲容器的进水管，打开它的出水管，甲容器只出水；到16分钟时，再次打开甲容器的进水管，此时甲容器既进水又出水；到28分钟时，关闭甲容器的出水管，并同时关闭甲、乙两容器的进水管．已知两容器每分钟的进水量与出水量均为常数，图中折线O-A-B-C和线段DE分别表示两容器内的水量(单位：升)与时间(单位：分)之间的函数关系，请根据图象回答下列问题：

(1) 甲容器的进水管每分钟进水______升，它的出水管每分钟出水______升；
(2) 求乙容器内的水量与时间的函数关系式；
(3) 求从初始时刻到最后一次两容器内的水量相等时所需的时间．

有一个装有进水管和出水管的容器，水管的所有阀门都处于关闭状态．初始时，打开容器的进水管，只进水；到5分钟时，打开容器的出水管，此时既进水又出水；到15分钟时，关闭容器的进水管，只出水；到分钟时，容器内的水全部排空．已知此容器每分钟的进水量与出水量均为常数，容器内的水量(单位：升)与时间(单位：分)之间的函数关系如图所示，请根据图象回答下列问题：

（1）此容器的进水管每分钟进水______升；
（2）求时，容器内的水量与时间的函数关系式；
（3）此容器的出水管每分钟出水多少升？的值为多少？

已知：直线与轴交于点A，与轴交于点B．
（1）分别求出A，B两点的坐标；
（2）过A点作直线AP与轴交于点P，且使OP=2OB，求△ABP的面积．

已知：如图1，长方形ABCD中，AB=2，动点P在长方形的边BC，CD，DA上沿的方向运动，且点P与点A，B都不重合．图2是此运动过程中，△ABP的面积与点P经过的路程之间的函数图象的一部分．

请结合以上信息回答下列问题：
（1）长方形ABCD中，边BC的长为________；
（2）若长方形ABCD中，M为CD边的中点，当点P运动到与点M重合时，=________，=________；
（3）当时，与之间的函数关系式是___________________；
（4）利用第（3）问求得的结论，在图2中将相应的与的函数图象补充完整．

如图，在直角三角形AOB中，∠OAB=30°，AB=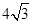，S_△AOB=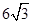.（1）求点A、B的坐标；
（2）点P在线段OA上
①当直线BP将△AOB分成面积相等的两部分时，求直线BP的解析式；
②PE⊥AB于E，连接BP.是否存在点P，使得PB与PE的和最小？若存在，请求出满足条件时点P的坐标；若不存在，请说明理由．

 

如图①，一条笔直的公路上有A、B、C三地，B、C两地相距 150 千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A地的距离、（千米）与行驶时间 x（时）的关系如图②所示．

根据图象进行以下探究：
（1）请在图①中标出 A地的位置，并作简要说明；
(2) 甲的速度为            ，乙的速度为         .
（3）求图②中M点的坐标，并解释该点的实际意义；
（4）在图②中补全甲车到达C地的函数图象，求甲车到 A地的距离与行驶时间x的函数关系式；
（5）出发多长时间，甲、乙两车距A点的距离相等？

如图，直线l₁的解析表达式为：，且l₁与x轴
交于点D，直线l₂经过点A，B，直线l₁，l₂交于点C．
（1）求直线l₂的函数关系式；
（2）求△ADC的面积；
（3）若点H为坐标平面内任意一点，在坐标平面内是否存在这样的点H，使以A、D、C、H为顶点的四边形是平行四边形？若存在，请直接写出点H的坐标；若不存在，请说明理由．

某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的收费y（元）与通讯时间x（分钟）之间的函数关系如图所示．

（1）有月租费的收费方式是   （填①或②），月租费是     元；
（2）分别求出①、②两种收费方式中收费y（元）与通讯时间x（分钟）之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出经济实惠的选择建议．

如图所示，在直角坐标系中，点是反比例函数的图象上一点，轴的正半轴于点，是的中点；一次函数的图象经过、两点，并交轴于点若

（1）求反比例函数和一次函数的解析式；
（2）观察图象，请指出在轴的右侧，当时的取值范围，当＜时的取值范围．

( 本题10分) 某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：

运输工具	运输费单价   （元/吨·千米）	冷藏费单价   （元/吨·小时）	过路费 （元）	装卸及管理费 （元）
汽车	2	5	200	0
火车	1.8	5	0	1600

     注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨·小时”表示每吨货物每小时的冷藏费．
（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y₁（元）和y₂（元），试求出y₁和y₂和与x的函数关系式；
（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？

在平面直角坐标系中，一动点P（，y）从M（1，0）出发，沿由A（-1，1），B（-1，-1），C（1，-1），D（1，1）四点组成的正方形边线（如图①）按一定方向运动。图②是P点运动的路程s（个单位）与运动时间（秒）之间的函数图象，图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.

（1）求s与之间的函数关系式。
（2）求与图③相对应的P点的运动路径；及P点出发多少秒首次到达点B；
（3）写出当3≤s≤8时，y与s之间的函数关系式，并在图③中补全函数图象.

如图，在平面直角坐标系中，直线l是第一、三象限的角平分线
实验与探究：

（1）由图观察易知A（0，2）关于直线l的对称点的坐标为（2，0），请在图中分别标明B(5,3)、C(-2,5) 关于直线l的对称点、的位置，并写出他们的坐标:             、             ；
归纳与发现：
（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为           
运用与拓广：
（3）已知两点D(1,-3)、E(-1,-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．