初中数学一次函数的最值解答题

（本题10分）已知一个正比例函数和一个一次函数的图象交于点P(－2,2),且一次函数的图象与y轴相交于点Q（0，4）
（1）求这两个函数的解析式
（2）在同一坐标系内，分别画出这两个函数的图象
（3）求出的面积

．(本题满分12分) 如图，在平面直角坐标系中，四边形OABC为直角梯形，OA∥BC，BC=14，A（16，0），C（0，2）.
(1)如图①，若点P、Q分别从点C、A同时出发，点P以每秒2个单位的速度由C向B运动，点Q以每秒4个单位的速度由A向O运动，当点Q停止运动时，点P也停止运动.设运动时间为t秒（0≤t≤4）.
①求当t为多少时，四边形PQAB为平行四边形？(4分)
②求当t为多少时，直线PQ将梯形OABC分成左右两部分的比为1:2，并求出此时直线PQ的解析式. (4分)
（2）如图②，若点P、Q分别是线段BC、AO上的任意两点（不与线段BC、AO的端点重合），且四边形OQPC面积为10，试说明直线PQ一定经过一定点，并求出该定点的坐标. (4分)

(本题满分10分) （1）观察与发现：将矩形纸片AOCB折叠，使点C与点A重合，点B落在点B′ 处(如图1)，折痕为EF．小明发现△ AEF为等腰三角形，你同意吗？请说明理由．(3分)

（2）实践与应用：以点O为坐标原点，分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系，若顶点B的坐标为（9，3），请求出折痕EF的长及EF所在直线的函数关系式．(4+3分)

 如图，已知直线AB与x轴交于A(6，0)点，与y轴交于B(0，10)点，点M的坐标为(0，4)，
点P(x，y)是折线O→A→B的动点(不与O点、B点重合)，连接OP、MP，设△OPM的面积为S．
 
(1) 求S关于x的函数表达式，并写x的取值范围；
(2) 当△OPM是以OM为底边的等腰三角形时，求S的值；
(3) 当线段MP分△OAB的面积比为1∶4时，求P点坐标．

2008年6月1日起，我国实施“限塑令”，开始有偿使用环保购物袋．为了满足市场需求，某厂家生产两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产种购物袋个，每天共获利元．

（1）求出与的函数关系式；
（2）如果该厂每天最多投入成本10000元，那么每天最多获利多少

（本题8分）小明上午7：05从家里出发以均匀的速度步行上学，途经少年宫时走了步，用时10分钟，7：30到达学校.为了估测路程等有关数据，小明特意在学校的田径跑道上，按上学的步行速度，走完100米用了150步．

(1)　小明上学步行的平均速度是　▲　米/分；小明家和少年宫之间的路程是　▲　米；少年宫和学校之间的路程是　▲　米．
(2)　下午4：00，小明从学校出发，以45米/分的速度行走，按上学时的原路回家，在未到少年宫300米处与同伴玩了半小时后，赶紧以110米/分的速度回家，中途没有再停留．问：
①　小明到家的时间是下午几时？
②　小明回家过程中，离家的路程s(米)与时间t(分)之间的函数关系如图，请写出点B的坐标，并求出线段CD所在直线的函数解析式．

如图，在平面直角坐标系xOy中，一条直线l与x轴相交于点A，
与y轴相交于点，与正比例函数 y＝mx(m≠0)的图象
相交于点．

（1）求直线l的解析式；（2）求△AOP的面积．

(本题满分10分) 今年“五一”期间，小明准备攀登海拔高度为2000米的山峰。导游介绍山区气温会随着海拔高度的增加而下降，提醒大家上山要多带一件衣服，小明从网上查到该山区海拔和即时气温的部分数据表，数据如下：

海拔高度x（米）	400	500	600	700	800	……
气温y（°C）	29.2	28.6	28.0	27.4	26.8	……

（1）以海拔高度为x轴，根据上表提供的数据在下列直角坐标系中描点并连线；

（2）观察(1)中所画出的图象，猜想与之间函数关系，求出所猜想的函数关系表达式，并根据表中提供的数据验证你的猜想；
（3）如果气温低于20⁰C就需要穿外套，请问小明需不需要携带外套上山？

(本题12分)如图①，平面直角坐标系中，已知C（0,10），点P、Q同时从点出发，在线段OC上做往返匀速运动，设运动时间为t(s)，点P、Q离开点O的距离为S图②中线段OA、OB（A、B都在格点上）分别表示当0≤t≤6时P、Q两点离开点O的距离S与运动时间t(s)的函数图像．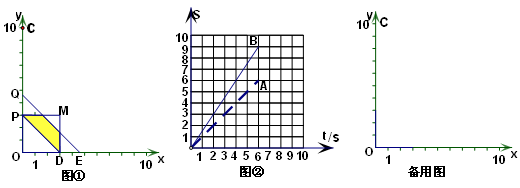

⑴请在图②中分别画出当6≤t≤10时P、Q两点离开点O的距离S与运动时间t(s)的函数图像．
⑵求出P、Q两点第一次相遇的时刻．
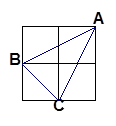
⑶如图①，在运动过程中，以OP为一边画正方形OPMD，点D在x轴正半轴上，作QE∥PD交x轴于E，设△PMD与△OQE重合部分的面积 为y，试求出当0≤t≤10时y与t(s)的函数关系式(写出相应的t的范围)．

(本题10分)某个体经营户销售同一型号的A、B两种品牌的服装，平均每月共销售60件，已知两种品牌的成本和利润如表所示，设平均每月的利润为y元，每月销售A品牌x件．

⑴写出y关于x的函数关系式．
⑵如果每月投入的成本不超过6500元，所获利润不少于2920元，不考虑其他因素，那么销售方案有哪几种？
⑶要使平均每月利润率最大，请直接写出A、B两种品牌的服装各销售多少件？

受国际原油价格持续上涨影响，某市对出租车的收费标准进行调整．

（1）调整前出租车的起步价为  ▲  元，超过3km收费  ▲ 元/km；
（2）求调整后的车费y（元）与行驶路程x（km）（x>3）之间的函数关系式，并在图中画出其函数图象．

某厂工人小王某月工作的部分信息如下：
信息一：工作时间：每天上午8∶20～12∶00，下午14∶00～16∶00，每月25天；
信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．
生产产品件数与所用时间之间的关系见下表：

生产甲产品件数（件）	生产乙产品件数（件）	所用总时间
10	10	350
30	20	850

信息三：按件计酬，每生产一件甲产品可得1.50元，每生产一件乙产品可得2.80元．
根据以上信息，回答下列问题：
（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分？
（2）小王该月最多能得多少元？此时生产甲、乙两种产品分别多少件？

已知：甲、乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到B地后立即返回，下图是它们离各自出发地的距离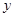（千米）与行驶时间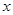（小时）之间的函数图象．

（1）求甲车离出发地的距离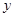（千米）与行驶时间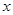（小时）之间的函数关系式，并写出自变量的取值范围；
（2）当它们行驶到与各自出发地的距离相等时，用了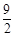小时，求乙车离出发地的距离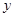（千米）与行驶时间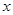（小时）之间的函数关系式，并写出自变量的取值范围；
（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．

如图，矩形ABCD的边AB在x轴上，AB的中点与原点O重合，AB=2，AD=1，点Q的坐标为(0，2)．

（1）求直线QC的解析式；
（2）点P(a，0)在边AB上运动，若过点P、Q的直线将矩形ABCD的周长分成3∶1两部分，求出此时a的值．

某航空公司经营A、B、C、D四个城市之间的客运业务. 若机票价格y(元)是两城市间的距离x(千米)的一次函数. 今年“清明节”期间部分机票价格如下表所示：

求该公司机票价格y(元)与距离x(千米)的函数关系式
判断A、B、C、D这四个城市中，哪三个城市在同一条直线上？请说明理由；
若航空公司准备从旅游旺季的7月开始增开从B市直接飞到D市的旅游专线，且按以上规律给机票定价，那么机票定价应是多少元？