如图,已知直线AB与x轴交于A(6,0)点,与y轴交于B(0,10)点,点M的坐标为(0,4),
点P(x,y)是折线O→A→B的动点(不与O点、B点重合),连接OP、MP,设△OPM的面积为S.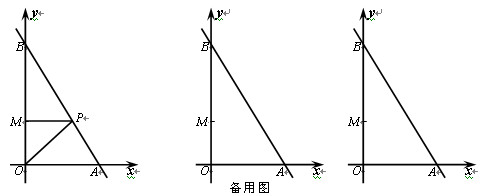
(1) 求S关于x的函数表达式,并写x的取值范围;
(2) 当△OPM是以OM为底边的等腰三角形时,求S的值;
(3) 当线段MP分△OAB的面积比为1∶4时,求P点坐标.
相关知识点
推荐套卷
如图,已知直线AB与x轴交于A(6,0)点,与y轴交于B(0,10)点,点M的坐标为(0,4),
点P(x,y)是折线O→A→B的动点(不与O点、B点重合),连接OP、MP,设△OPM的面积为S.
(1) 求S关于x的函数表达式,并写x的取值范围;
(2) 当△OPM是以OM为底边的等腰三角形时,求S的值;
(3) 当线段MP分△OAB的面积比为1∶4时,求P点坐标.