利达经销店为某工厂代销一种建筑材料(这里的代销指厂家先免费提供货源,待货物销售后再进行结算,末售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高利润,准备采取降价的方式进行促销.经市场调查发现: 当每吨售价每下降10元时, 月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其
他费用100元.设每吨材料售价为x(元), 该经销店的月销售量y(元).
该经销店的月销售量y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的关系式(不要求写出x的取值范围);
(3)该经销店要获得最大利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大”,你认为对吗?请说明理由.
如图1,平面直角坐标系 xOy中,A
xOy中,A ,B
,B .将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿
.将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿 轴负方向平移m个单位得到△EFG(m>0,O,A,B的
轴负方向平移m个单位得到△EFG(m>0,O,A,B的 对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数
对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数 (k≠0)的图象上.
(k≠0)的图象上.
(1)∠AOB=" " °,a=" " °;
(2)求经过点A,B,F的抛物线的解析式;
(3)若(2)中抛物线的顶点为M,抛物线与直线EF的另一个交点为H,抛物线上的点P满足以P,M,F,A为顶点的四边形的面积与四边形MFAH的面积相等(点P不与点H重合),请直接写出满足条件的点P的个数,并求位于直线EF上方的点P 的坐标.
的坐标.
抛物线 ,a>0,c<0,
,a>0,c<0, .
.
(1)求证: ;
;
(2)抛物线经过点 ,Q
,Q .
.
① 判断 的符号;
的符号;
② 若抛物线与x轴的两个交点分别为点A ,点B
,点B (点A在点B左侧),请说明
(点A在点B左侧),请说明 ,
, .
.
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
已知关于x的方程(m-1)x2-(2m-1)x+2=0有两个正整数根.
(1) 确定整数m值;
(2) 在(1)的条件下,利用图象写出方程(m-1)x2-(2m-1)x+2+ =0的实数根的个数.
=0的实数根的个数.
某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: .根据公司信息部的报告,
.根据公司信息部的报告, ,
, (万元)与投资金额
(万元)与投资金额 (万元)的部分对应值如下表所示:
(万元)的部分对应值如下表所示:
 |
1 |
5 |
 |
0.8 |
4 |
 |
3.8 |
15 |
(1)填空: ;
; ;
;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额x之间的函数关系式;
(3)请你设计一个在⑵中能获得最大利润的投资方案.
如图,在平面直角坐标系中,点A的坐标为(1, ) ,点B在x轴的负半轴上,
) ,点B在x轴的负半轴上,
∠ABO=30°.
(1)求过点A、O、B的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使AC+OC的值最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)在(1)中 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
已知:二次函数y=2x2+bx+c过点(1,1)和点(2,10),求二次函数的解析式,并用配
方法求二次函数图象的顶点坐标。
如图,抛物线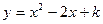 与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.
与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.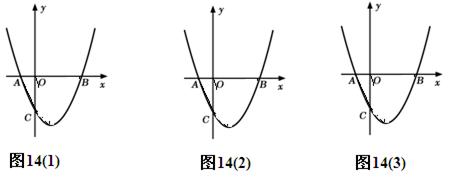
(1)k=_______,点A的坐标为___________,点C的坐标为_____________.
(2)设抛物线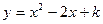 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
如图9,在平面直角坐标系中,二次函数 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=

(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图10,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
如图,直线 分别与x轴、y轴交于A、B两点;直线
分别与x轴、y轴交于A、B两点;直线 与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位
与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位 ),点E的运动时间为t(秒).
),点E的运动时间为t(秒).
⑴求点C的坐标.
⑵当0<t<5时,求S与t之间的函数关系式.
⑶求⑵中S的最大值.
⑷当t>0时,直接写出点(4, )在正方形PQMN内部时t的取值范围.
)在正方形PQMN内部时t的取值范围.
.某商店在1-10月份的时间销售A、B两种电子产品,已知产品A每个月的售价  (元)
(元)
与月份  (
(  且
且  为整数)之间的关系可用如下表格表示:
为整数)之间的关系可用如下表格表示:
时间  (月) (月) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
售价  (元) (元) |
720 |
360 |
240 |
180 |
144 |
120 |
120 |
120 |
120 |
120 |
已知产品A的进价为140元/件,A产品的销量  (件)与月份
(件)与月份  的关系式为
的关系式为  已知B产品的进价为450元/件,产品B的售价
已知B产品的进价为450元/件,产品B的售价  (元)与月份
(元)与月份  (
(  且
且  为整数)之间的函数关系式为
为整数)之间的函数关系式为  ,产品B的销量
,产品B的销量  (件)与月份
(件)与月份  的关系可用如下的图像反映.
的关系可用如下的图像反映.
已知该商店每个月需固定支出500元的物管杂费以及5个员工的工资,已知员工每人每月的工资为1500元.请结合上述信息解答下列问题:

(1)请观察表格与图像,用我们所学习的一次函数,反比例函数,或者二次函数写出  与
与  的
的
函数关系式,  与
与  的函数关系式;
的函数关系式;
(2)试表示出商店每月销售A、B两种产品的总利润  (将每月必要的开支除去)与月份
(将每月必要的开支除去)与月份  的
的
函数关系式,并求出该商店在哪个月时获得最大利润;
(3)为了鼓励员  工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常的
工的积极性,在最后4个月的销售期间商店老板决定奖励员工,除了正常的
工资外,每卖一件A产品,每个员工都提成0.75元,每卖一件B产品每个员工都提成10
元,这样A产品的销量将每月减少  件,而B产品的销量将每月增加
件,而B产品的销量将每月增加  件;请问在第几月时总利润(除去当月所有支出部分)可达到16750元?
件;请问在第几月时总利润(除去当月所有支出部分)可达到16750元?
(参考数据:  )
)
如图,抛物线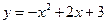 与
与 轴相交于
轴相交于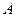 、
、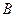 两点(点
两点(点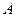 在点
在点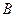 的左侧),与
的左侧),与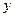 轴相交于点
轴相交于点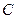 ,顶点为
,顶点为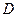 .
.
(1)直接写出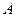 、
、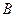 、
、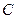 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)连接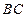 ,与抛物线的对
,与抛物线的对 称轴交于点
称轴交于点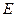 ,点
,点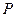 为线段
为线段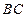 上的一个动点,过点
上的一个动点,过点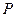 作
作 交抛物线于点
交抛物线于点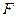 ,设点
,设点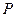 的横坐标为
的横坐标为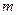 ;
;
①用含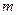 的代数式表示线段
的代数式表示线段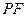 的长,并求出当
的长,并求出当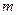 为何值时,四边形
为何值时,四边形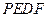 为平行四边形?
为平行四边形?
②设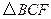 的面积为
的面积为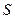 ,求
,求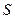 与
与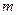 的函数关系式
的函数关系式
已知二次函数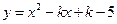 .
.
⑴求证:无论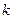 取何实数,此二次函数的图像与
取何实数,此二次函数的图像与 轴都有两个交点;
轴都有两个交点;
⑵若此二次函数图像的对称轴为 ,求它的解析式;
,求它的解析式;