初中数学二次函数在给定区间上的最值解答题

（1）解方程：4x2-8x-3=0
（2）求抛物线与x轴和y轴的交点坐标．

如图，抛物线y=ax²+bx+c的顶点为C（0，﹣），与x轴交于点A、B，连接AC、BC，得等边△ABC．T点从B点出发，以每秒1个单位的速度向点A运动，同时点S从点C出发，以每秒个单位的速度向y轴负方向运动，TS交射线BC于点D，当点T到达A点时，点S停止运动．设运动时间为t秒．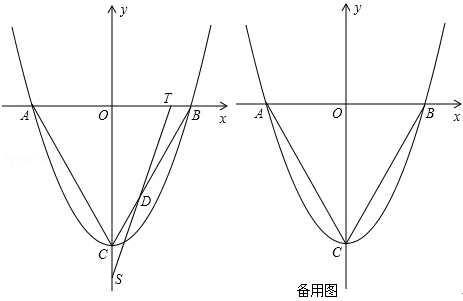

（1）求二次函数的解析式；
（2）设△TSC的面积为S，求S关于t的函数解析式；
（3）以点T为圆心，TB为半径的圆与射线BC交于点E，试说明：在点T运动的过程中，线段ED的长是一定值，并求出该定值．

已知二次函数y=x²﹣2bx+c的图象与x轴只有一个交点．
（1）请写出b、c的关系式；
（2）设直线y=7与该抛物线的交点为A、B，求AB的长；
（3）若P（a，﹣a）不在抛物线y=x²﹣2bx+c上，请求出b的取值范围．

如图，二次函数y=ax²+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长．

如图，在平面直角坐标系中，抛物线与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=－1．

（1）求抛物线对应的函数关系式；
（2）动点Ｑ从点O出发，以每秒1个单位长度的速度在线段OA上运动，同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动．过点Ｑ作x轴的垂线交线段AB于点N，交抛物线于点P，设运动的时间为t秒
①当t为何值时，四边形OMPＱ为矩形；
②△AON能否为等腰三角形？若能，求出t的值；若不能，请说明理由．

某公司营销A、B两种产品，根据市场调研，发现如下信息：
信息1：销售A种产品所获利润y（万元）与销售量x（吨）之间存在二次函数关系y=ax²+bx．在x=1时，y=1．4；当x=3时，y=3．6．
信息2：销售B种产品所获利润y（万元）与销售量x（吨）之间存在正比例函数关系y=0．3x．
根据以上信息，解答下列问题；
（1）求二次函数解析式；
（2）该公司准备购进A、B两种产品共10吨，请设计一个营销方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少？

已知抛物线
（1）填空：抛物线的顶点坐标是（   ，     ），对称轴是           ；
（2）已知y轴上一点A（0，-2），点P在抛物线上，过点P作PB⊥x轴，垂足为B．若△PAB是等边三角形，求点P的坐标；
（3）在（2）的条件下，点M在直线AP上．在平面内是否存在点 N，使以点O、点A、点M、点N为顶点的四边形为菱形？若存在，直接写出所有满足条件的点N的坐标；若不存在，请说明理由． 

某水果批发商场经销一种水果，如果每千克盈利10元，每天可售出400千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）当每千克涨价为多少元时，每天的盈利最多？最多是多少？
（2）若商场只要求保证每天的盈利为4420元，同时又可使顾客得到实惠，每千克应涨价为多少元？

二次函数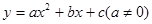的图象如图所示，根据图象解答下列问题：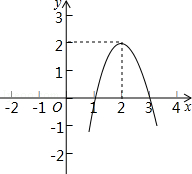

（1）写出方程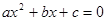的两个根；
（2）当x为何值时，y＞0；y＜0？
（3）写出y随x的增大而减小的自变量x的取值范围．

（本题8分）已知抛物线的图象经过点（﹣1，0），点（3，0）；
（1）求抛物线函数解析式；（2）求函数的顶点坐标．

如图，在直角坐标平面内，直线y=－x+5与轴和轴分别交于A、B两点，二次函数y=+bx+c的图象经过点A、B，且顶点为C．

（1）求这个二次函数的解析式；
（2）求sin∠OCA的值；
（3）若P是这个二次函数图象上位于x轴下方的一点，且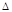ABP的面积为10，求点P的坐标．

已知二次函数y=ax²＋bx－3的图象经过点A（2，－3），B（－1，0）．求二次函数的解析式

如图，在直角坐标系中，抛物线经过点A（0，4），B（1，0），C（5，0），其对称轴与x轴相交于点M．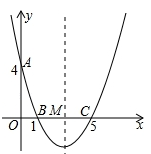

（1）求抛物线的解析式和对称轴；
（2）在抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由．

已知二次函数
（1）求它的顶点坐标和对称轴；
（2）画出这个函数的图象；
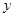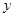（3）根据图象回答：当取哪些值时，＝0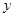，＞0，＜0