初中数学二次函数在给定区间上的最值解答题

如图，王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线y=－，其中y（m）是球的飞行高度，x（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．
（1）请写出抛物线的开口方向、顶点坐标、对称轴．
（2）请求出球飞行的最大水平距离．
（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式

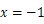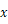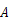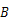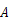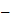对称轴为直线  的抛物线y =x²+bx+c，与轴相交于，两点，其中点的坐标为（3，0）．

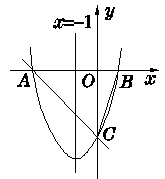
（1）求点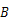的坐标．
（2）点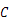是抛物线与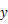轴的交点，点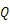是线段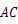上的动点，作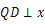轴交抛物线于点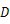，求线段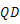长度的最大值．

已知：如图，二次函数的图象与x轴交于A（﹣2，0），B（4，0）两点，且函数的最大值为9．

（1）求二次函数的解析式；
（2）设此二次函数图象的顶点为C，与y轴交点为D，求四边形ABCD的面积．

如图，在平面直角坐标系中，抛物线y=﹣x²+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是矩形，点A的坐标为（1，0），点B的坐标为（0，4），已知点E（m，0）是线段DO上的动点，过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．

（1）求该抛物线的解析式；
（2）当点P在直线BC上方时，请用含m的代数式表示PG的长度；
（3）在（2）的条件下，是否存在这样的点P，使得以P、B、G为顶点的三角形与△DEH相似？若存在，求出此时m的值；若不存在，请说明理由．

（本题14分）如图①，已知抛物线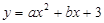（a≠0）与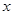轴交于点A（1，0）和点B（－3，0），与y轴交于点C．

（1）求抛物线的解析式；
（2）设抛物线的对称轴与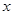轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．

本题14分）利达经销店为某工厂代销一种建筑材料（这里的代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7．5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其它费用共100元．设每吨材料售价为x（元），该经销店的月利润为y（元）．
（1）当每吨售价是240元时，计算此时的月销售量；
（2）求出y与x的函数关系式（不要求写出x的取值范围）；
（3）该经销店要获得最大月利润，售价应定为每吨多少元？
（4）小静说：“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．

某公司生产的某种时令商品每件成本为20 元，经过市场调研发现，这种商品在未来40天内的日销售量Q（件）与时间t（天）的关系如下表：

时间（天）	1	3	6	10	36	…
日销售量（件）	94	90	84	76	24	…

 
未来40天内，前20天每天的价格y₁（元/件）与时间t（天）的函数关系式为：y₁=t+25（1≤t≤20且t为整数）；后20天每天的价格y₂（元/件）与时间t（天）的函数关系式为：y₂=﹣t+40（21≤t≤40且t为整数）．
（1）求Q（件）与时间t（天）的函数关系式；
（2）请预测未来40天中哪一天的销售利润最大，最大日销售利润是多少？
（3）在实际销售的前20天中该公司决定每销售一件商品就捐赠a元利润（a＜4）给希望工程，公司通过销售记录发现，前20 天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求a的取值范围．

如图1，已知：抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，经过B，C两点的直线是y=x-2，连结AC．

（1）求出抛物线的函数关系式；
（2）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
（3）点P（t，0）是x轴上一动点，P、Q两点关于直线BC成轴对称，PQ交BC于点M，作QH⊥x轴于点H．连结OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．

基本模型
如图1，点A，F，B在同一直线上，若∠A=∠B=∠EFC=90°，易得△AFE∽△BCF．
（1）模型拓展：
如图2，点A，F，B在同一直线上，若∠A=∠B=∠EFC，求证：△AFE∽△BCF；
（2）拓展应用：如图3，AB是半圆⊙O的直径，弦长AC=BC=4，E，F分别是AC，AB上的一点，若∠CFE=45°．若设AE=y，BF=x，求出y与x的函数关系式及y的最大值；
（3）拓展提升：如图4，在平面直角坐标系柳中，抛物线y=﹣（x+4）（x﹣6）与x轴交于点A，C，与y轴交于点B，抛物线的对称轴交线段BC于点E，探求线段AB上是否存在点F，使得∠EFO=∠BAO？若存在，求出BF的长；若不存在，请说明理由．

如图1，已知：抛物线y=x²+bx+c与x轴交于A，B两点，与y轴交于点C，经过B，C两点的直线是y=x-2，连结AC．

（1）求出抛物线的函数关系式；
（2）若△ABC内部能否截出面积最大的矩形DEFC（顶点D、E、F、G在△ABC各边上）？若能，求出在AB边上的矩形顶点的坐标；若不能，请说明理由．
（3）点P（t，0）是x轴上一动点，P、Q两点关于直线BC成轴对称，PQ交BC于点M，作QH⊥x轴于点H．连结OQ，是否存在t的值，使△OQH与△APM相似？若存在，求出t的值；若不存在，说明理由．

如图，抛物线y=ax²+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．

（1）求抛物线的解析式；
（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；

某企业生产的一批产品上市后30天内全部售完，调查发现，国内市场的日销售量为y₁（吨）与时间t（t为整数，单位：天）的关系如图1所示的抛物线的一部分，而国外市场的日销售量y₂（吨）与时间t，t为整数，单位：天）的关系如图2所示．

（1）求y₁与时间t的函数关系式及自变量t的取值范围，并写出y₂与t的函数关系式及自变量t的取值范围；
（2）设国内、国外市场的日销售总量为y吨，直接写出y与时间t的函数关系式，当销售第几天时，国内、外市场的日销售总量最早达到75吨？
（3）判断上市第几天国内、国外市场的日销售总量y最大，并求出此时的最大值．

如图，已知抛物线y=x²+mx+n（n≠0）与直线y=x交于A、B两点，与y轴交于点C，OA=OB，BC∥x轴．

（1）求抛物线的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（点E在点D的上方），DE=，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．

下表中所列x，y的数值是某二次函数y=ax²+bx+c图象上的点所对应的坐标，其中x₁＜x₂＜x₃＜x₄＜x₅＜x₆＜x₇，根据表中所提供的信息，以下判断正确的是（ ）．
①a＞0；
②9＜m＜16；
③k≤9；
④b²≤4a（c﹣k）．

x	…	x1	x2	x3	x4	x5	x6	x7	…
y	…	16	m	9	k	9	m	16	…

A．①②    B．③④    C．①②④    D．①③④

已知，如图，二次函数y=ax²+2ax﹣3a（a≠0）图象的顶点为H，与x轴交于A、B两点（B在A点右侧），点H、B关于直线l：对称．

（1）求A、B两点坐标，并证明点A在直线l上；
（2）求二次函数解析式；
（3）过点B作直线BK∥AH交直线l于K点，M、N分别为直线AH和直线l上的两个动点，连接HN、NM、MK，求HN+NM+MK和的最小值．