如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．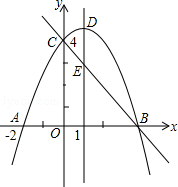
（1）求抛物线的解析式；
（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
的图象经过第一、二、四象限，求m的取值范围 .
相关知识点
推荐套卷
如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．
（1）求抛物线的解析式；
（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；
粤公网安备 44130202000953号