初中数学二次函数在给定区间上的最值试题

如图，把抛物线y=x²与直线y=1围成的图形OABC绕原点O顺时针旋转90°后，再沿x轴向右平移1个单位得到图形O₁A₁B₁C₁，则下列结论错误的是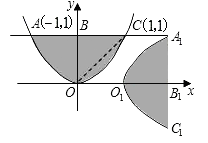

A．点O1的坐标是（1，0）

B．点C1的坐标是（2，-1）

C．四边形OBA1B1是矩形

D．若连接OC，则梯形OCA1B1的面积是3

已知抛物线y=ax²+bx+c经过（-1，0），（2，0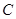），（0，2）三点．

（1）求这条抛物线的解析式；
（2）如图①，点P是第一象限内此抛物线上的一个动点，当点P运动到什么位置时，四边形ABPC的面积最大？求出此时点P的坐标；
（3）如图②，设线段AC的垂直平分线交x轴于点E，垂足为D，M为抛物线的顶点，那么在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由．

在平面直角坐标系中，二次函数（）的图象可能是（ ）

A．

B．

C．

D．

抛物线y=x²+2x+3的顶点坐标是         ．

二次函数y=a的图象如图所示，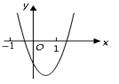

则一次函数y=bx+与反比例函数y=在同一坐标系内的图象大致为（     ）

如图，抛物线y=-x²+2x+m+1交x轴于点A（a，0）和B（B，0），交y轴于点C，抛物线的顶点为D．下列四个判断：①当x>0时，y>0；②若a=-1，则b=4；③抛物线上有两点P（x_1,y₁）和Q（x_2,y₂），若x₁<1< x₂，且x₁+ x₂>2，则y₁> y₂；④点C关于抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为，其中正确判断的序号是（  ）

（A）①     （B）②
（C）③     （D）④

把二次函数y=2x的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为            ．

二次函数的图象如图所示，则下列说法不正确的是（   ）

A．

B．

C．

D．

如果二次函数的图象如图所示，对称轴x=-1，下列五个代数式ab、ac、a-b+c、b-4ac、2a+b中，值大于0的个数为（  ）

A．5

B．4

C．3

D．2

二次函数的最大值为（ ）

A．3

B．4

C．5

D．6

已知抛物线（）过（﹣2，0），（2，3）两点，那么抛物线的对称轴（ ）

A．只能是x=﹣1

B．可能是y轴

C．在y轴右侧且在直线x=2的左侧

D．在y轴左侧且在直线x=﹣2的右侧

已知抛物线y＝ax²＋bx＋c（a＞0）过（－2，0），（2，3）两点，那么抛物线的对称轴（  ）

A．只能是x=－1

B．可能是y轴

C．在y轴右侧且在直线x=2的左侧

D．在y轴左侧且在直线x=－2的右侧

在下列二次函数中，其图象的对称轴为的是（     ）

A．	B．
C．	D．

下列函数解析式中，一定为二次函数的是（     ）

A．	B．
C．	D．

设抛物线与x轴的交点为A（， 0），B（，0），其中，点P（m，n）为抛物线上一动点，连接AP，BP．，当∠APB为锐角时，下列m的取值范围中正确的是_________；（填序号）
① m＜-1 ② -1＜m＜0 ③ o＜m＜3 ④ 3＜m＜4 ⑤ m＞4