初中数学二次函数在给定区间上的最值试题

图2是图1中拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可近似看成抛物线，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴，若OA=10米，则桥面离水面的高度AC为（ ）

A．米

B．米

C．米

D．米

抛物线y=ax²+bx+c的图象如图所示，则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为（ ）

如图，已知二次函数（）的图象与x轴交于点A（﹣1，0），对称轴为直线x=1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：
①当x＞3时，y＜0；
②3a+b＜0；
③；
④；
其中正确的结论是（ ）

A．①③④

B．①②③

C．①②④

D．①②③④

在同一坐标系中，一次函数y=ax+2与二次函数y=x²+a的图象可能是（ ）

如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E，已知CD=8，抛物线经过O、E、A三点．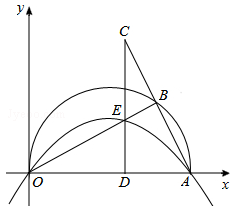

（1）∠OBA=       °；
（2）求抛物线的函数表达式；
（3）若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个？

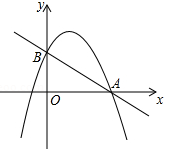
如图，已知二次函数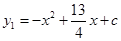的图象与x轴的一个交点为A（4，0），与y轴的交点为B，过A、B的直线为．

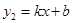（1）求二次函数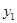的解析式及点B的坐标；
（2）由图象写出满足的自变量x的取值范围；
（3）在两坐标轴上是否存在点P，使得△ABP是以AB为底边的等腰三角形？若存在，求出P的坐标；若不存在，说明理由．

抛物线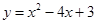与x轴交于A、B两点（点A在点B的左侧），点C是此抛物线的顶点．
（1）求点A、B、C的坐标；
（2）点C在反比例函数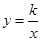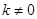（）的图象上，求反比例函数的解析式．

如图，在平面直角坐标系中，⊙A与x轴相交于C（﹣2，0），D（﹣8，0）两点，与y轴相切于点B（0，4）．

（1）求经过B，C，D三点的抛物线的函数表达式；
（2）设抛物线的顶点为E，求证：直线CE与⊙A相切；
（3）在x轴下方的抛物线上，是否存在一点F，使△BDF面积最大，最大值是多少？并求出点F的坐标．

二次函数y=ax²+bx+c（a≠0）的图象与x轴交于A（-3，0）、B（1，0）两点，与y轴交于点C（0，-3m）（其中m＞0），顶点为D．
（1）用含m的代数式分别表示a、b、c；
（2）如图，当m取何值时，△ADC为直角三角形？

如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P沿折线BE﹣ED﹣DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒．设P、Q同时出发t秒时，△BPQ的面积为ycm²．已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分）．则下列结论错误的是（      ）

A．

B．当时，∽

C．

D．当时，

已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表：

x	…	-1	0	1	2	3	…
y	…	-6	-1	2	3	2	…

 
则当y＜-1时，x的取值范围是            ．

如图，二次函数y=x（x-2）（0≤x≤2）的图象，记为C₁，它与x轴交于O、A₁两点；将C₁绕点A₁旋转180°得C₂，交x轴于点A₂；将C₂绕点A₂旋转180°得C₃，交x轴于点A₃；…如此进行下去，直至得C₂₀₁₆．若P（4031，m）在第2016段图象C₂₀₁₆上，则m=         ．

小明开了一家网店，进行社会实践，计划经销甲、乙两种商品．若甲商品每件利润10元，乙商品每件利润20元，则每周能卖出甲商品40件，乙商品20件．经调查，甲、乙两种商品零售单价分别每降价1元，这两种商品每周可各多销售10件．为了提高销售量，小明决定把甲、乙两种商品的零售单价都降价x元．
（1）直接写出甲、乙两种商品每周的销售量y（件）与降价x（元）之间的函数关系式：y_甲=               ，y_乙=               ；
（2）求出小明每周销售甲、乙两种商品获得的总利润W（元）与降价x（元）之间的函数关系式？如果每周甲商品的销售量不低于乙商品的销售量的，那么当x定为多少元时，才能使小明每周销售甲、乙两种商品获得的总利润最大？

写一个你喜欢的实数m的值                     ，使得事件“对于二次函数，当时，y随x的增大而减小”成为随机事件．

如果二次函数的图象如图所示，那么一次函数和反比例函数在同一坐标系中的图象大致是（ ）

A．

B．

C．

D．