2015年初中毕业升学考试(甘肃庆阳卷)数学
2015羊年春晚在某网站取得了同时在线人数超14 000 000的惊人成绩,创下了全球单平台网络直播记录,则14 000 000用科学记数法可表示为( )
| A.0.14×108 | B.1.4×107 | C.1.4×108 | D.14×106 |
下列说法属于不可能事件的是( )
| A.四边形的内角和为360° |
| B.梯形的对角线不相等 |
| C.内错角相等 |
D.存在实数x满足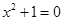 |
某几何体由一些大小相同的小正方体组成,如图分别是它的主视图和俯视图,那么要组成该几何体,至少需要多少个这样的小正方体( )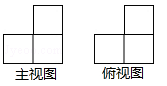
| A.3 | B.4 | C.5 | D.6 |
已知点P( ,
, )关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A. |
B. |
C. |
D. |
如图是二次函数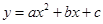 图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )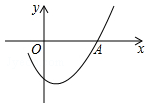
A.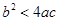 |
B.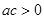 |
C.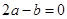 |
D.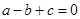 |
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )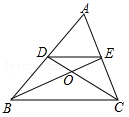
| A.1:4 | B.1:3 | C.1:2 | D.2:3 |
如果二次函数 的图象如图所示,那么一次函数
的图象如图所示,那么一次函数 和反比例函数
和反比例函数 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )
A. |
B. |
C. |
D. |
在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )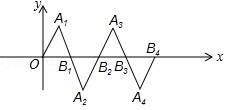
A.(4n﹣1,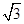 ) ) |
B.(2n﹣1,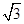 ) ) |
C.(4n+1,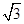 ) ) |
D.(2n+1,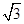 ) ) |
如图,Rt△ABC中,∠ACB=90°,AC=BC= ,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为 (结果保留π).
,若把Rt△ABC绕边AB所在直线旋转一周,则所得几何体的表面积为 (结果保留π).
有六张完全相同的卡片,其正面分别标有数字:﹣2,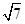 ,
,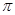 ,0,
,0, ,
,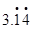 ,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
,将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数字为无理数的概率是 .
已知三条不同的直线a、b、c在同一平面内,下列四条命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm.(结果保留π)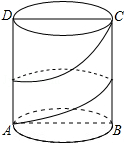
如图,在△ABC中,∠C=60°,∠A=40°.
(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
解答下列问题:
(1)图中D所在扇形的圆心角度数为 ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.
(1)当AB=2时,求△GEC的面积;
(2)求证:AE=EF.
某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.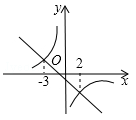
(1)max{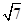 ,3}= ;
,3}= ;
(2)已知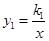 和
和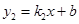 在同一坐标系中的图象如图所示,若max{
在同一坐标系中的图象如图所示,若max{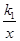 ,
,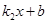 }=
}=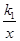 ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;
(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6, 时,求DE的长.
时,求DE的长.
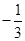 的相反数是( )
的相反数是( )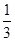




 ,则∠C的大小是( )
,则∠C的大小是( )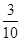
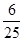
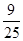
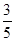
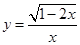 的自变量x的取值范围是 .
的自变量x的取值范围是 . 的平方根是 .
的平方根是 .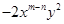 与
与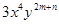 是同类项,则
是同类项,则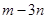 的立方根是 .
的立方根是 .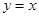 上运动,当线段AB最短时,点B的坐标为 .
上运动,当线段AB最短时,点B的坐标为 .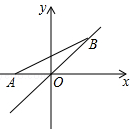
 .
.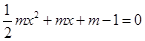 有两个相等的实数根.
有两个相等的实数根.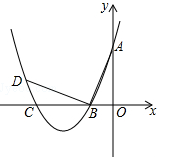
 粤公网安备 44130202000953号
粤公网安备 44130202000953号