初中数学二次函数在给定区间上的最值试题

宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现：如果单独投资A种产品，则所获利润（万元）与投资金额（万元）之间满足正比例函数关系：；如果单独投资B种产品，则所获利润（万元）与投资金额（万元）之间满足二次函数关系：.根据公司信息部的报告，，（万元）与投资金额（万元）的部分对应值（如下表）

（1）填空：
_______________________；
_______________________；
（2）如果公司准备投资20万元同时开发A、B两种新产品，设公司所获得的总利润为（万元），试写出与某种产品的投资金额x之间的函数关系式.
（3）请你设计一个在（2）中能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少万元？

小明从如图所示的二次函数的图象中，观察得出了下面五条信息：①；②；③；④；⑤. 你认为其中正确信息的个数有

A．2个

B．3个

C．4个

D．5个

将二次函数的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是

A．	B．
C．	D．

温州市有一种可食用的野生菌，上市时，外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将以每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这类野生菌在冷库中最多保存160天，同时，平均每天有3千克的野生菌损坏不能出售。
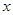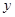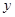设天后每千克该野生菌的市场价格为元，试写出与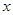之间的函数关系式；
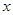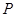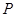若存放天后，将这批野生菌一次性出售，设这批野生菌的销售总额为元，试写出与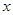之间的函数关系式；
李经理将这批野生菌存放多少天后出售可获得最大利润元？
（利润＝销售总额－收购成本－各种费用）

一座拱型桥，桥下水面宽度AB是20米，拱高CD是4米．若水面上升3米至EF，则水面宽度EF是多少？

若把它看作是抛物线的一部分，在坐标系中（如图1）可设抛物线的表达式为．请你填空：a=       ，c=        ，EF=            米．
若把它看作是圆的一部分，则可构造图形（如图2）计算如下：
设圆的半径是r米，在Rt△OCB中，易知，r=14.5
同理，当水面上升3米至EF，在Rt△OGF中可计算出GF=     米，即水面宽度EF=      米．

二次函数的图象如图所示，则下列结论中
①a<0  b>0  c>0  ; ②4a+2b+c="3" ; ③ ; ④;
⑤当x<2时，y随x的增大而增大. 正确的个数是：（    ）

A．1个

B．2个

C．3个

D．4个

开口向的抛物线的顶点P的坐标是（1，－3），则此抛物线对应的二次函数有
(       )

A．最大值1

B．最小值－1

C．最大值－3

D．最小值3

将抛物线向左平移5个单位，再向上平移3个单位后得到的抛物线的解析式为_______________________．

如图，抛物线y=x²+bx+c经过A（－1，0），B（4，5）两点，请
解答下列问题：
求抛物线的解析式；
若抛物线的顶点为点D，对称轴所在的直线交x轴于点E，连接AD，点F为AD的中点，求出线段EF的长。
注：抛物线y=ax²+bx+c的对称轴是x=，顶点坐标是（，）。

如图，在平面直角坐标系中，点A、B、C、P的坐标分别为（0，1）、
（－1，0）、（1，0）、（－1，－1）。
求经过A、B、C三点的抛物线的表达式；
以P为位似中心，将△ABC放大，使得放大后的△A₁B₁C₁与△OAB对应线段的比为3：1，请在右图网格中画出放大后的△A₁B₁C₁；（所画△A₁B₁C₁与△ABC在点P同侧）；
经过A₁、B₁、C₁三点的抛物线能否由（1）中的抛物线平移得到？请说明理由。

如图是抛物线y=ax²+bx+c的一部分，其对称轴为直线x=1，若其与x轴一交点为B
（3，0），则由图像可知，不等式ax²+bx+c＞0的解集是        x＜-1或x＞3。

若y=(m+1)是二次函数，则m的值为              。

已知抛物线y=(m－1)x²，且直线y=3x+3－m经过一、二、三象限，则m的范围是       。

如图，已知的顶点，，是坐标原点．将绕点按逆时针旋转90°得到．

写出两点的坐标；
求过三点的抛物线的解析式，并求此抛物线的顶点的坐标；
在线段上是否存在点使得？若存在，请求出点的坐标；若不存在，请说明理由．

一个二次函数的图象顶点坐标为（4，3），形状与开口方向和抛物线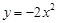相同，
这个函数解析式为                               .