2011年三校联考九年级上学期期中考试数学卷
如图,点A、B、C在⊙O上,∠ACB=20°,则∠AOB的度数是( )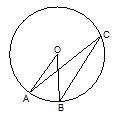
A、1O° B、20° C、40° D、70°
圆锥母线长为3cm.底面半径为2cm,则其侧面展开图的面积是( )
| A.12πcm2 | B.6 cm2 | C.3cm2 | D.6πcm2 |
某班某同学要测量学校升旗的旗杆高度,在同一时刻,量得某一同学的身高是1.5m,影长是1m,旗杆的影长是8m,则旗杆的高度是( )
| A.12m | B.11m | C.10m | D.9m |
已知二次函数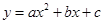 的图象如图所示,则
的图象如图所示,则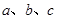 满足 ( )
满足 ( )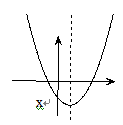
A、a>0,b>0,c<0 B、a>0,b<0,c<0
C、a<0,b>0,c>0 D、a>0,b<0,c>0
如图,∠APD=90°,AP=PB=BC=CD,则下列结论成立的是( )
| A.ΔPAB∽ΔPDA | B.ΔABC∽ΔDCA |
| C.ΔPAB∽ΔPCA | D.ΔABC∽ΔDBA |
△ABC的三条边之比为2:5:6,与其相似的另一个△A′B′C′最大边长为18cm,
则△A′B′C′的最短边长为___ ____cm.
某商场销售一批羊毛衫,每天可售出20件,每件盈利50元,据市场分析,如果一件羊毛
衫每降价1元,每天可多售出2件,针对这种销售情况,每件羊毛衫降价 元
时,商场一天销售这种羊毛衫的盈利达到最大.
如图, △ABC中,AB=AC=3cm,BC=2cm,以AC为直径作半圆交AB于点D,交BC于点E,则图中[阴影部分面积为 cm2.
如图,已知反比例函数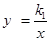 和正比例函数
和正比例函数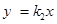 的图像的一个交点为
的图像的一个交点为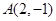 .
.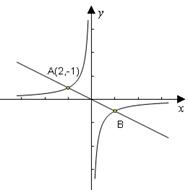
求反比例函数和正比例函数的解析式.
求反比例函数和正比例函数的图像的另一个交点B的坐标.
一条排水管的截面如右图所示,截面中有水部分弓形的弦AB为 cm, 弓形的高为6cm.
cm, 弓形的高为6cm.求截面⊙O的半径.
求截面中的劣弧AB的长.

如图,D,E分别是△ABC的AB,AC边上的点,且DE∥BC,已知AD︰DB=1︰3, DE=2cm,求BC的长.
若△ADE的面积为1.5cm2,求梯形DBCE的面积.

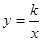 (
(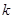 ≠0)的图象经过点(2,-3),那么
≠0)的图象经过点(2,-3),那么 )
)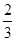
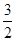
 写成比例式,写错的是( )
写成比例式,写错的是( )



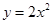 向右平移3个单位,再向上平移5个单位,则得到的抛物线是 ( )
向右平移3个单位,再向上平移5个单位,则得到的抛物线是 ( )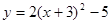
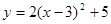
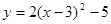
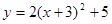
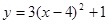 的对称轴是直线( )
的对称轴是直线( )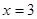

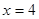
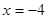
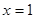

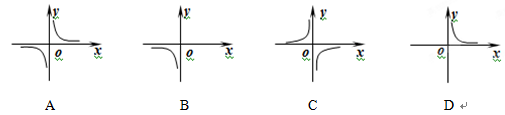
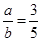 ,那么
,那么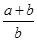 等于 .
等于 .
 的二次函数
的二次函数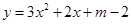 的图象经过原点,则
的图象经过原点,则 = .
= . 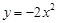 相同,
相同,


 ,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,
,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,
 的顶点
的顶点 ,
, ,
, 是坐标原点.将
是坐标原点.将 .
.
 两点的坐标;
两点的坐标; 三点的抛物线的解析式,并求此抛物线的顶点
三点的抛物线的解析式,并求此抛物线的顶点 的坐标;
的坐标; 上是否存在点
上是否存在点 使得
使得 ?若存在,请求出点
?若存在,请求出点 粤公网安备 44130202000953号
粤公网安备 44130202000953号