初中数学二次函数在给定区间上的最值试题

求二次函数的顶点坐标(＿＿＿)对称轴＿＿＿＿。

若抛物线y=x²-6x+c-2的顶点到x轴的距离是3,则c的值等于（  ）

A．8; 或14

B．14;

C．-8

D．-8或-14

抛物线的图像如图，则下列结论
①＞0；         ②；
③；④其中正确的结论是 (     )
 

A．①②

B．②③④

C．②④

D．③④

抛物线y=x²的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（     ）

A．y=x^2+4x+3

B．y=x^2+4x+5

C．y=x^2－4x+3

D．y=x^2－4x－5

下列函数不属于二次函数的是 （    ）

A．y=(x－1)(x+2)

B．y=1－x^2

C．y=(x+1)^2

D．y=2(x+3)^2－2x^2

已知抛物线y＝ax²＋bx＋c(a≠0)在平面直角坐标系中的位置如图所示，则下列结论中正确的是(  )

A．a>0

B．b＜0

C．c＜0

D．a＋b＋c>0

若二次函数y=ax²+bx+c的x与y的部分对应值如下表：

则当x=1时，y的值为（   ）

A．5

B．-3

C．-13

D．-27

(本题满分10分)正常水位时，抛物线拱桥下的水面宽为20m，水面上升3m达到该地警戒水位时，桥下水面宽为10m．
（1）在恰当的平面直角坐标系中求出水面到桥孔顶部的距离y（m）与水面宽x（m）之间的函数关系式；
（2）如果水位以0.2m/h的速度持续上涨，那么达到警戒水位后，再过多长时间此桥孔将被淹没？

(本题满分10分)已知函数y=mx²－6x＋1（m是常数）．
⑴求证：不论m为何值，该函数的图象都经过y轴上的一个定点；
⑵若该函数的图象与x轴只有一个交点，求m的值．

(本题满分8分)已知抛物线与x轴没有交点．
(1)求c的取值范围；
(2)试确定直线y＝cx+l经过的象限，并说明理由．

(本题满分8分)写出二次函数的图像顶点坐标和对称轴的位置，求出它的最大值或最小值，并画出它的图像。

将二次函数化为的形式，则          ．

如图，已知二次函数的图象经过点（-1，0），（1，-2），该图象与x轴的另一个交点为C，则AC长为　  　．

将抛物线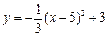向左平移5个单位，再向上平移3个单位后得到的抛物线的解析式为_______________________．

抛物线交轴于、两点，交轴于点，顶点为.

（1）写出抛物线的对称轴及、两点的坐标（用含的代数式表示）
（2）连接并以为直径作⊙，当时，请判断⊙是否经过点，并说明理由；
（3）在（2）题的条件下，点是抛物线上任意一点，过作直线垂直于对称轴，垂足为. 那么是否存在这样的点，使△与以、、为顶点的三角形相似？若存在，请求出点的坐标；若不存在，请说明理由.