初中数学二次函数在给定区间上的最值试题

已知二次函数y=ax²+bx+c(a≠0)的图象如图所示，有下列5个结论：①abc＜0；②a－b+c＞0；③ 2a+b=0；④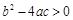 ⑤a+b+c＞m(am+b)+c，（m＞1的实数），其中正确的结论有（   ）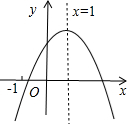

A．1个

B．2个

C．3个

D．4个

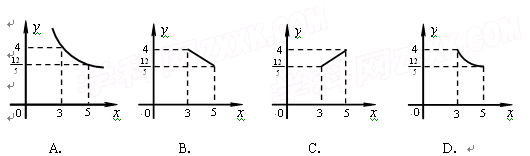
如图，在矩形ABCD中，AB＝4，BC＝3，点P在CD边上运动，联结AP，过点B作BE⊥AP，垂足为E，设AP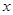＝，BE＝，则能反映与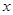之间函数关系的图象大致是（   ）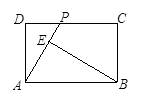

将抛物线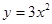先向左平移2个单位，再向下平移1个单位后得到新的抛物线，则
新抛物线的解析式是（    ）

A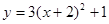．	B．
C．	D．

如图11所示，已知抛物线与轴交于A、B两点，与轴交于点C．

求A、B、C三点的坐标
过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
在轴上方的抛物线上是否存在一点M，过M作MG轴于点G，使以A、M、G三点为顶点的三角形与PCA相似．若存在，请求出M点的坐标；否则，请说明理由．

如图，已知：抛物线，关于轴对称；抛物线，关于轴对称。
如果抛物线的解析式是，那么抛物线的解析式
是                  ．

已知直角梯形纸片OABC在平面直角坐标系中的位置如图①所示，四
个顶点的坐标分别为O(0，0)，A(10，0)，B(8，2)，C(0，2)，点P在线段OA上(不与O、A重合)，将纸片折叠，使点A落在射线AB上(记为点A’)，折痕PQ与射线AB交于点Q，设OP＝x，折叠后纸片重叠部分的面积为y．(图②供探索用)
求∠OAB的度数；
求y与x的函数关系式，并写出对应的x的取值范围；
y存在最大值吗？若存在，求出这个最大值，并求此时x的值；若不存在，说明理由．

)图①中是一座钢管混凝土系杆拱桥，桥的拱肋ACB可视为抛物线的一部分(如图②)，桥面(视为水平的)与拱肋用垂直于桥面的系杆连接，测得拱肋
的跨度AB为200米，与AB中点O相距20米处有一高度为48米的系杆．
求正中间系杆OC的长度；
若相邻系杆之间的间距均为5米(不考虑系杆的粗细)，则是否存在一根系杆的长度恰好是OC长度的一半？请说明理由．

已知二次函数y=ax²+2x+c，函数y与自变量x的部分对应值如下表：

x	……	－2	－1	0	1	2	……
y	……	－5	0	3	4	3	……

求这个二次函数的关系式；
请判断函数有最大值还是最小值，并写出此时x的值与y的值；
若y≥0，则x的取值范围是_______．
若A(n，y₁)、B(n+1，y₂)两点均在该函数的图象上，试比较y₁与y₂大小．

（本小题满分5分）二次函数中，自变量与函数的对

x	-1	-	0		1		2		3
y	-2	-	1		2		1	-	-2

应值如表：
判断二次函数图像的开口方向，写出它的顶点坐标。
一元二次方程的两个根的取值范围是下
列选项中的哪一个____________
①     ②
③     ④

（本小题满分5分）已知二次函数图象的顶点坐标是（1，-4），且与y轴交于点
（0，-3）,求此二次函数的解析式.

如图，二次函数的图象开口向上，图象经过点和，且与轴相交于负半轴，给出四个结论：①；②；③；④.其中正确的序号是                      

已知：，且=0，则二次函数的图象可能是下列图象中的（   ）．    

已知抛物线y＝－x²＋2x＋3的顶点为P，与x轴的两个交点为A，B，那么△ABP的面积等于          

将二次函数y＝x²－2的图象向左平移2个单位，再向上平移1个单位，所得抛物线的解析式为                     

若抛物线C：y＝ax²＋bx＋c与抛物线y＝x²－2关于x轴对称，则抛物线C的解析式为

A．y＝x^2－2	B．y＝－x^2－2
C．y＝－x^2＋2	D．y＝x^2＋2