初中数学列表法与树状图法解答题

随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有 $A$、 $B$、 $C$、 $D$、 $E$等著名景点，该市旅游部门统计绘制出2017年“五 $·$一”长假期间旅游情况统计图，根据以下信息解答下列问题：

（1）2017年“五 $·$一”期间，该市周边景点共接待游客　　万人，扇形统计图中 $A$景点所对应的圆心角的度数是　　，并补全条形统计图．

（2）根据近几年到该市旅游人数增长趋势，预计2018年“五 $·$一”节将有80万游客选择该市旅游，请估计有多少万人会选择去 $E$景点旅游？

（3）甲、乙两个旅行团在 $A$、 $B$、 $D$三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明，并列举所有等可能的结果．

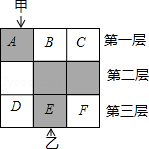
如图， $3\times 3$的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格 $A$、 $B$、 $C$中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格 $D$、 $E$、 $F$中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

（1）若乙固定在 $E$处，移动甲后黑色方块构成的拼图是轴对称图形的概率是　　．

（2）若甲、乙均可在本层移动．

①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．

②黑色方块所构拼图是中心对称图形的概率是　　．

如图， $3\times 3$的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格 $A$、 $B$、 $C$中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格 $D$、 $E$、 $F$中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

（1）若乙固定在 $E$处，移动甲后黑色方块构成的拼图是轴对称图形的概率是　　．

（2）若甲、乙均可在本层移动．

①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．

②黑色方块所构拼图是中心对称图形的概率是　　．

在四个完全相同的小球上分别标上 1 ， 2 ， 3 ， 4 四个数字， 然后装入一个不透明的口袋里搅匀， 小明同学随机摸取一个小球记下标号， 然后放回， 再随机摸取一个小球， 记下标号 ．

（1） 请你用画树状图或列表的方法分别表示小明同学摸球的所有可能出现的结果 ．

（2） 按照小明同学的摸球方法， 把第一次取出的小球的数字作为点 $M$的横坐标， 把第二次取出的小球的数字作为点 $M$的纵坐标， 试求出点 $M(x,y)$落在直线 $y=x$上的概率是多少？

2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛，在全州安全知识竞赛结束后，通过网上查询，某校一名班主任对本班成绩（成绩取整数，满分100分）作了统计分析，绘制成如下频数分布表和频数分布直方图，请你根据图表提供的信息，解答下列问题：

（1）频数分布表中 $a=$　　， $b=$　　， $c=$　　

（2）补全频数分布直方图

（3）为了激励学生增强安全意识，班主任准备从超过90分的学生中选2人介绍学习经验，那么取得100分的小亮和小华同时被选上的概率是多少？请用列表法或画树状图加以说明，并列出所有等可能结果．

频数分布表

分组（分 $)$	频数	频率
$50<x$ 60	2	0.04
$60<x$ 70	12	$a$
$70<x<80$	$b$	0.36
$80<x$ 90	14	0.28
$90<x$ 100	$c$	0.08
合计	50	1

为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”．比赛项目为： $A$．唐诗； $B$．宋词； $C$．论语； $D$．三字经．比赛形式分“单人组”和“双人组”．

（1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？

（2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．

黔东南州某中学为了解本校学生平均每天的课外学习实践情况，随机抽取部分学生进行问卷调查，并将调查结果分为 $A$， $B$， $C$， $D$四个等级，设学习时间为 $t$（小时）， $A:t<1$， $B:1⩽t<1.5$， $C:1.5⩽t<2$， $D:t⩾2$，根据调查结果绘制了如图所示的两幅不完整的统计图．请你根据图中信息解答下列问题：

（1）本次抽样调查共抽取了多少名学生？并将条形统计图补充完整；

（2）本次抽样调查中，学习时间的中位数落在哪个等级内？

（3）表示 $B$等级的扇形圆心角 $\alpha$的度数是多少？

（4）在此次问卷调查中，甲班有2人平均每天课外学习时间超过2小时，乙班有3人平均每天课外学习时间超过2小时，若从这5人中任选2人去参加座谈，试用列表或画树状图的方法求选出的2人来自不同班级的概率．

教室里有4排日光灯，每排灯各由一个开关控制，但灯的排数序号与开关序号不一定对应，其中控制第二排灯的开关已坏（闭合开关时灯也不亮）．

（1）将4个开关都闭合时，教室里所有灯都亮起的概率是　　；

（2）在4个开关都闭合的情况下，不知情的雷老师准备做光学实验，由于灯光太强，他需要关掉部分灯，于是随机将4个开关中的2个断开，请用列表或画树状图的方法，求恰好关掉第一排与第三排灯的概率．

某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：

（1）这次调查的学生共有多少名？

（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．

（3）如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为 $A$、 $B$、 $C$、 $D$、 $E)$．

今年5月13日是“母亲节”，某校开展“感恩母亲，做点家务”活动为了了解同学们在母亲节这一天做家务情况，学校随机抽查了部分同学，并用得到的数据制成如下不完整的统计表：

做家务时间（小时）	人数	所占百分比
$A$组：0.5	15	$30\%$
$B$组：1	30	$60\%$
$C$组：1.5	$x$	$4\%$
$D$组：2	3	$6\%$
合计	$y$	$100\%$

（1）统计表中的 $x=$　　， $y=$　　；

（2）小君计算被抽查同学做家务时间的平均数是这样的：

第一步：计算平均数的公式是 $\bar{x}=\frac{x_1+x_2+x_3+\dots +x_n}{n}$，

第二步：该问题中 $n=4$， $x_1=0.5$， $x_2=1$， $x_3=1.5$， $x_4=2$，

第三步： $\bar{x}=\frac{0.5+1+1.5+2}{4}=1.25$（小时）

小君计算的过程正确吗？如果不正确，请你计算出正确的做家务时间的平均数；

（3）现从 $C$， $D$两组中任选2人，求这2人都在 $D$组中的概率（用树形图法或列表法）．

箱子里有4瓶牛奶，其中有一瓶是过期的．现从这4瓶牛奶中不放回地任意抽取2瓶．

（1）请用树状图或列表法把上述所有等可能的结果表示出来；

（2）求抽出的2瓶牛奶中恰好抽到过期牛奶的概率．

九年级（1）班全班50名同学组成五个不同的兴趣爱好小组，每人都参加且只能参加一个小组，统计（不完全）人数如下表：

编号	一	二	三	四	五
人数	$a$	15	20	10	$b$

已知前面两个小组的人数之比是 $1:5$．

解答下列问题：

（1） $a+b=$　　．

（2）补全条形统计图：

（3）若从第一组和第五组中任选两名同学，求这两名同学是同一组的概率．（用树状图或列表把所有可能都列出来）

某校七、八年级各有10名同学参加市级数学竞赛，各参赛选手的成绩如下（单位：分） $:$

七年级：89，92，92，92，93，95，95，96，98，98

八年级：88，93，93，93，94，94，95，95，97，98

整理得到如下统计表：

年级	最高分	平均分	众数	方差
七年级	98	94	$m$	7.6
八年级	98	94	93	$s^2$

根据以上信息，完成下列问题：

（1）填空： $m=$　　；

（2）求表中 $s^2$的值，并判断两个年级中哪个年级成绩更稳定；

（3）七年级两名最高分选手分别记为： $A_1$， $A_2$，八年级第一、第二名选手分别记为： $B_1$， $B_2$，现从这四人中，任意选取两人参加市级经验交流，请用树状图法或列表法求出这两人分别来自不同年级的概率．

在“植树节”期间，小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动，规则如下：在两个盒子内分别装入标有数字1，2，3，4的四个和标有数字1，2，3的三个完全相同的小球，分别从两个盒子中各摸出一个球，如果所摸出的球上的数字之和小于6，那么小王去，否则就是小李去．

（1）用树状图或列表法求出小王去的概率；

（2）小李说：“这种规则不公平”，你认同他的说法吗？请说明理由．

九 （1）班48名学生参加学校举行的“珍惜生命，远离毒品”知识竞赛初赛，赛后，班长对成绩进行分析，制作如下的频数分布表和频数分布直方图（未完成）．余下8名学生成绩尚未统计，这8名学生成绩如下：60，90，63，99，67，99，99，68．

频数分布表

分数段	频数（人数）
$60⩽x<70$	$a$
$70⩽x<80$	16
$80⩽x<90$	24
$90⩽x<100$	$b$

请解答下列问题：

（1）完成频数分布表， $a=$　　， $b=$　　．

（2）补全频数分布直方图；

（3）全校共有600名学生参加初赛，估计该校成绩 $90⩽x<100$范围内的学生有多少人？

（4）九 （1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲、乙两位同学的概率．