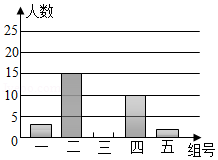
九年级（1）班全班50名同学组成五个不同的兴趣爱好小组，每人

九年级（1）班全班50名同学组成五个不同的兴趣爱好小组，每人都参加且只能参加一个小组，统计（不完全）人数如下表：

编号	一	二	三	四	五
人数	$a$	15	20	10	$b$

已知前面两个小组的人数之比是 $1 : 5$ ．

解答下列问题：

（1） $a + b =$ 　　．

（2）补全条形统计图：

（3）若从第一组和第五组中任选两名同学，求这两名同学是同一组的概率．（用树状图或列表把所有可能都列出来）

登录免费查看答案和解析

相关试题

如图，已知 $D$ 为 $⊙ O$ 上一点，点 $C$ 在直径 $B A$ 的延长线上， $B E$ 与 $⊙ O$ 相切，交 $C D$ 的延长线于点 $E$ ，且 $B E ＝ D E$ ．

（1）判断 $C D$ 与 $⊙ O$ 的位置关系，并说明理由；

（2）若 $A C ＝ 4$ ， $\sin C = \frac{1}{3}$ ，

①求 $⊙ O$ 的半径；

②求 $B D$ 的长．

收藏答案/解析

为落实国家“双减”政策，立德中学在课后托管时间里开展了“音乐社团、体育社团、文学社团、美术社团”活动．该校从全校 $600$ 名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动（每人必选且只选一种）”的问卷调查，根据调查结果，绘制了如图所示的两幅不完整的统计图．

根据图中信息，解答下列问题：

（1）参加问卷调查的学生共有＿＿＿＿人；

（2）条形统计图中m的值为＿＿＿＿，扇形统计图中 $α$ 的度数为＿＿＿＿；

（3）根据调查结果，可估计该校 $600$ 名学生中最喜欢“音乐社团”的约有＿＿＿＿人；

（4）现从“文学社团”里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛，请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率．

收藏答案/解析

如图，在平行四边形 $A B C D$ 中，点 $E ， F$ 分别在边 $A B ， C D$ 上，且四边形 $B E D F$ 为正方形．

（1）求证： $A E ＝ C F$ ；

（2）已知平行四边形 $A B C D$ 的面积为 $20$ ， $A B ＝ 5$ ，求 $C F$ 的长．

收藏答案/解析

已知关于 $x$ 的一元二次方程 $x^{2} + （ 2 k + 1 ） x + k^{2} + 1 ＝ 0$ 有两个不等实数根 $x_{1} ， x_{2}$ ．

（1）求 $k$ 的取值范围；

（2）若 $x_{1} x_{2} ＝ 5$ ，求 $k$ 的值．

收藏答案/解析

解分式方程： $\frac{1}{x} = \frac{4}{x + 3}$ ．

收藏答案/解析