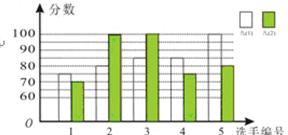
某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为 、 、 、 、 .
推荐套卷
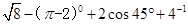 ;
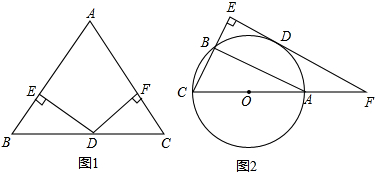
;

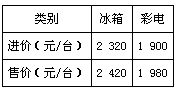
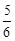 . 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少?
. 若使商场获利最大,请你帮助商场计算应该购进冰箱、彩电各多少台?最大获利是多少? 粤公网安备 44130202000953号
粤公网安备 44130202000953号