初中数学概率公式解答题

端午节那天，小贤回家看到桌上有一盘粽子，其中有豆沙粽、肉粽各1个，蜜枣粽2个，这些粽子除馅外无其他差别．

（1）小贤随机地从盘中取出一个粽子，取出的是肉粽的概率是多少？

（2）小贤随机地从盘中取出两个粽子，试用画树状图或列表的方法表示所有可能的结果，并求出小贤取出的两个都是蜜枣粽的概率．

6月14日是“世界献血日”，某市采取自愿报名的方式组织市民义务献血．献血时要对献血者的血型进行检测，检测结果有“ $A$型”、“ $B$型”、“ $\mathit{AB}$型”、“ $O$型”4种类型．在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表：

血型	$A$	$B$	$\mathit{AB}$	$O$
人数		10	5

（1）这次随机抽取的献血者人数为　　人， $m=$　　；

（2）补全上表中的数据；

（3）若这次活动中该市有3000人义务献血，请你根据抽样结果回答：

从献血者人群中任抽取一人，其血型是 $A$型的概率是多少？并估计这3000人中大约有多少人是 $A$型血？

如图，甲、乙两人（看成点）分别在数轴和5的位置上，沿数轴做移动游戏．每次移动游戏规则：裁判先捂住一枚硬币，再让两人猜向上一面是正是反，而后根据所猜结果进行移动．

①若都对或都错，则甲向东移动1个单位，同时乙向西移动1个单位；

②若甲对乙错，则甲向东移动4个单位，同时乙向东移动2个单位；

③若甲错乙对，则甲向西移动2个单位，同时乙向西移动4个单位．

（1）经过第一次移动游戏，求甲的位置停留在正半轴上的概率；

（2）从如图的位置开始，若完成了10次移动游戏，发现甲、乙每次所猜结果均为一对一错．设乙猜对次，且他最终停留的位置对应的数为，试用含的代数式表示，并求该位置距离原点最近时的值；

（3）从如图的位置开始，若进行了次移动游戏后，甲与乙的位置相距2个单位，直接写出的值．

杨老师为了了解所教班级学生课后复习的具体情况，对本班部分学生进行了一个月的跟踪调查，然后将调查结果分成四类： $A$：优秀； $B$：良好； $C$：一般； $D$：较差．并将调查结果绘制成以下两幅不完整的统计图．

请根据统计图解答下列问题：

（1）本次调查中，杨老师一共调查了　      　名学生，其中 $C$类女生有　    　名， $D$类男生有　         　名；

（2）补全上面的条形统计图和扇形统计图；

（3）在此次调查中，小平属于 $D$类．为了进步，她请杨老师从被调查的 $A$类学生中随机选取一位同学，和她进行“一帮一”的课后互助学习．请求出所选的同学恰好是一位女同学的概率．

编号为号的5名学生进行定点投篮，规定每人投5次，每命中1次记1分，没有命中记0分，如图是根据他们各自的累积得分绘制的条形统计图．之后来了第6号学生也按同样记分规定投了5次，其命中率为．

（1）求第6号学生的积分，并将图增补为这6名学生积分的条形统计图；

（2）在这6名学生中，随机选一名学生，求选上命中率高于的学生的概率；

（3）最后，又来了第7号学生，也按同样记分规定投了5次，这时7名学生积分的众数仍是前6名学生积分的众数，求这个众数，以及第7号学生的积分．

为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”．比赛项目为： $A$．唐诗； $B$．宋词； $C$．论语； $D$．三字经．比赛形式分“单人组”和“双人组”．

（1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？

（2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．

如图1，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字1，2，3，4．如图2，正方形 $\mathit{ABCD}$ 顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．

如：若从圈 $A$ 起跳，第一次掷得3，就顺时针连续跳3个边长，落到圈 $D$ ；若第二次掷得2，就从 $D$ 开始顺时针连续跳2个边长，落到圈 $B$ ； $\dots$

设游戏者从圈 $A$ 起跳．

（1）嘉嘉随机掷一次骰子，求落回到圈 $A$ 的概率 $P_1$ ；

（2）淇淇随机掷两次骰子，用列表法求最后落回到圈 $A$ 的概率 $P_2$ ，并指出她与嘉嘉落回到圈 $A$ 的可能性一样吗？

汤姆斯杯世界男子羽毛球团体赛小组赛比赛规则：两队之间进行五局比赛，其中三局单打，两局双打，五局比赛必须全部打完，赢得三局及以上的队获胜．假如甲，乙两队每局获胜的机会相同．

（1）若前四局双方战成 $2:2$，那么甲队最终获胜的概率是　　；

（2）现甲队在前两局比赛中已取得 $2:0$的领先，那么甲队最终获胜的概率是多少？

学校召集留守儿童过端午节，桌上摆有甲、乙两盘粽子，每盘中盛有白粽2个，豆沙粽1个，肉粽1个（粽子外观完全一样）．

（1）小明从甲盘中任取一个粽子，取到豆沙粽的概率是　　；

（2）小明在甲盘和乙盘中先后各取了一个粽子，请用树状图或列表法求小明恰好取到两个白粽子的概率．

从一副普通的扑克牌中取出四张牌，它们的牌面数字分别为2，3，3，6．

（1）将这四张扑克牌背面朝上，洗匀，从中随机抽取一张，则抽取的这张牌的牌面数字是3的概率为 　　；

（2）将这四张扑克牌背面朝上，洗匀．从中随机抽取一张，不放回，再从剩余的三张牌中随机抽取一张．请根据画树状图或列表的方法，求抽取的这两张牌的牌面数字恰好相同的概率．

一张圆桌旁设有4个座位，丙先坐在了如图所示的座位上，甲、乙2人等可能地坐到①、②、③中的2个座位上．

（1）甲坐在①号座位的概率是 　 　；

（2）用画树状图或列表的方法，求甲与乙相邻而坐的概率．

甲、乙两个家庭来到以“生态资源，绿色旅游”为产业的美丽云南，各自随机选择到大理、丽江、西双版纳三个城市中的一个城市旅游．假设这两个家庭选择到哪个城市旅游不受任何因素影响，上述三个城市中的每一个被选到的可能性相同，甲、乙两个家庭选择到上述三个城市中的同一个城市旅游的概率为 $P$．

（1）直接写出甲家庭选择到大理旅游的概率；

（2）用列表法或树状图法（树状图也称树形图）中的一种方法，求 $P$的值．

将图中的 $A$型、 $B$型、 $C$型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．

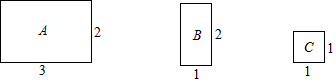
（1）搅匀后从中摸出1个盒子，求摸出的盒子中是 $A$型矩形纸片的概率；

（2）搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）．

某超市为庆祝开业举办大酬宾抽奖活动，凡在开业当天进店购物的顾客，都能获得一次抽奖的机会，抽奖规则如下：在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球，它们的形状、大小、质地完全相同，顾客先从盒子里随机取出一个小球，记下小球上标有的数字，然后把小球放回盒子并搅拌均匀，再从盒子中随机取出一个小球，记下小球上标有的数字，并计算两次记下的数字之和，若两次所得的数字之和为8，则可获得50元代金券一张；若所得的数字之和为6，则可获得30元代金券一张；若所得的数字之和为5，则可获得15元代金券一张；其他情况都不中奖．

（1）请用列表或树状图（树状图也称树形图）的方法（选其中一种即可），把抽奖一次可能出现的结果表示出来；

（2）假如你参加了该超市开业当天的一次抽奖活动，求能中奖的概率 $P$ ．

如图， $3\times 3$的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格 $A$、 $B$、 $C$中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格 $D$、 $E$、 $F$中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

（1）若乙固定在 $E$处，移动甲后黑色方块构成的拼图是轴对称图形的概率是　　．

（2）若甲、乙均可在本层移动．

①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．

②黑色方块所构拼图是中心对称图形的概率是　　．