今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
| 植树数量(棵) |
频数(人) |
频率 |
| 3 |
5 |
0.1 |
| 4 |
20 |
0.4 |
| 5 |
|
|
| 6 |
10 |
0.2 |
| 合计 |
50 |
1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图(折线图中,粗线表示甲,细线表示乙):

(1)根据图中所提供的信息填写下表:
| |
平均数 |
众数 |
方差 |
| 甲 |
7 |
|
|
| 乙 |
|
|
2.2 |
(2)请从下列四个不同的角度对测试结果进行分析:
①从平均数和方差结合看_______的成绩好;
②从平均数和众数结合看_______的成绩好;
③从折线图上两人射击环数的走势看_____更有潜力.
④如果你是教练,会选择哪位运动员参加比赛?说明理由.
(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
| 时间分组(小时) |
频数(人数) |
频率 |
| 0≤t<0.5 |
10 |
0.2 |
| 0.5≤t<1 |
|
0.4 |
| 1≤t<1.5 |
10 |
0.2 |
| 1.5≤t<2 |
|
0.1 |
| 2≤t<2.5 |
5 |
|
| 合计 |
|
1 |
请你将频数分布表和频数分布直方图补充完整.
国家环保局统一规定,空气质量分为5级.当空气污染指数达0—50时为1级,质量为优;51—100时为2级,质量为良;101—200时为3级,轻度污染;201—300时为4级,中度污染;300以上时为5级,重度污染.某城市随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
(1)本次调查共抽取了_______天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为________°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天)
翔志学校抽样调查后得到n名学生年龄情况,将结果绘制成如下的扇形统计图。
(1)被调查学生年龄的中位数是_______岁;
(2)通过计算求该学校学生年龄的平均数(精确到1岁);
(3)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数。
某校为了解该校九年级学生对蓝球、乒乓球、羽毛球、足球四种球类运动项目的喜爱情况,对九年级部分学生进行了随机抽样调查,每名学生必须且只能选择最喜爱的一项运动项目,将调查结果统计后绘制成如图两幅不完整的统计图,请根据图中的信息,回答下列问题:

(1)这次被抽查的学生有 人;请补全条形统计图;
(2)在统计图2中,“乒乓球”对应扇形的圆心角是 度;
(3)若该校九年级共有480名学生,估计该校九年级最喜欢足球的学生约有 人.
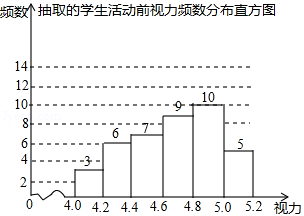
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到 ;活动后,再次检查这部分学生的视力,结果如表所示.
分组 |
频数 |
|
2 |
|
3 |
|
5 |
|
8 |
|
17 |
|
5 |
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
君畅中学计划购买一些文具送给学生,为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中,你最需要的文具是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据以上信息回答下列问题: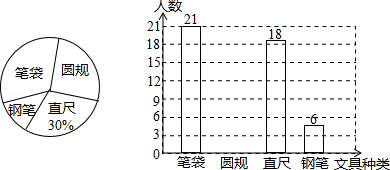
(1)在这次调查中,最需要圆规的学生有多少名?并补全条形统计图;
(2)如果全校有970名学生,请你估计全校学生中最需要钢笔的学生有多少名?
我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况,随机抽样调查了实验中学七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校七年级学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)如果我市共有七年级学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.请根据图中提供的信息解答下列问题
(1)这次共调查了多少名学生?扇形统计图中方案1所对应的圆心角的度数为多少度?
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人?
以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2(统计图不完整).请根据图中提供的信息,解答下列问题:
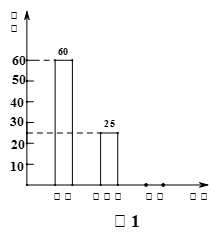
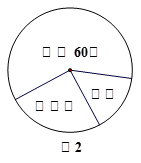
(1)此次抽样调查中,共抽查了 名学生;
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该校3000名学生中有多少名学生持反对态度?
下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
| 成绩 |
60 |
70 |
80 |
90 |
100 |
| 人数(人) |
1 |
5 |
x |
y |
2 |
(1)若这20名学生的平均分是84分,求x和y的值;
(2)这20名学生的本次测验成绩的众数和中位数分别是多少?
小龙在学校组织的社会调查活动中负责了解他所居住的小区500户居民的家庭收入情况。他从中随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图。
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于或等于1000不足1600元)的大约有多少户?
| 分组 |
频数 |
百分比 |
| 600≤x<800 |
2 |
5% |
| 800≤x<1000 |
6 |
15% |
| 1000≤x<1200 |
|
45% |
| 1200≤x<1400 |
9 |
22.5% |
| 1400≤x<1600 |
|
|
| 1600≤x<1800 |
2 |
5% |
| 合计 |
40 |
100% |

某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.