湖北省宜昌市(城区)八年级下学期期末考试数学试卷
要使代数式 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
| A.x≥2 | B.x≥-2 | C.x≤-2 | D.x≤2 |
已知甲,乙两班学生一次数学测验的方差分别为S甲2=154,S乙2=92,这两个班的学生成绩比较整齐的是( )
| A.乙班 | B.甲班 | C.两班一样 | D.无法确定 |
关于正比例函数y=-2x,下列说法错误的是( )
| A.图象经过原点 | B.图象经过第二,四象限 |
| C.y随x增大而增大 | D.点(2,-4)在函数的图象上 |
下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
A.1,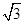 ,2 ,2 |
B.1,2,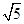 |
| C.5,12,13 | D.1,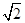 , ,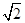 |
已知点A(-5,y1)和B(-4,y2)都在直线y=x-4上,则y1与y2的大小关系是( )
| A.y1>y2 | B.y1=y2 | C.y1<y2 | D.不能确定 |
如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )
| A.15° | B.22.5° | C.30° | D.45° |

一次函数y=-2x-4的图象不经过的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为( )
| A.9 | B.12 | C.15 | D.18 |
对某班6名同学进行体育达标测试,成绩分别是:80,90,75,80,75,80。关于这组数据,下列说法错误的是( )
| A.众数是80 | B.平均数是80 | C.中位数是75 | D.方差是25 |
如图,菱形ABCD的周长为20,一条对角线AC长为8,另一条对角线BD长为( )
| A.16 | B.12 | C.6 | D.4 |

在下列命题中,真命题是( )
| A.有两边平行的四边形是平行四边形 |
| B.对角线互相垂直平分的四边形是菱形 |
| C.有一个角是直角的四边形是矩形 |
| D.有一个角是直角且有一组邻边相等的四边形是正方形 |
如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),关于x的不等式x+m>kx-1的解集是( )
| A.x≥-1 | B.x>-1 | C.x≤-1 | D.x<-1 |

蜡烛燃烧时余下的长度y(cm) 和燃烧的时间x(分钟)的关系如图所示。
(1)求燃烧50分钟后蜡烛的长度;
(2)这支蜡烛最多能燃烧多长时间。
正方形ABCD中,AB=4,对角线交于点O,F是BO的中点,连接AF,求AF的长度。
翔志学校抽样调查后得到n名学生年龄情况,将结果绘制成如下的扇形统计图。
(1)被调查学生年龄的中位数是_______岁;
(2)通过计算求该学校学生年龄的平均数(精确到1岁);
(3)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数。
如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF。
(1)求证:2EF=CD;
(2)当EF与BC满足_____时,四边形ABCD是矩形;
(3)当EF与BC满足_____时,四边形ABCD是菱形,并证明你的结论;
(4)当EF与BC满足_____时,四边形ABCD是正方形。
翔志琼公司修筑一条公路,开始修筑若干天以后,公司抽调了一部力量去完成其他任务,所以施工速度有所降低。修筑公路的里程y(千米)和所用时间x(天)的关系用下图所示的折线OAB表示,其中OA所在的直线是函数y=0.1x的图象,AB所在直线是函数y= 的图象。
的图象。
(1)求点A的坐标;
(2)完成修路工程后,公司发现如果一直按开始的速度修筑此公路,可提前20天完工,求此公路的长度。
已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和边OA上,将△BOE沿着OE对折,使点B落在OC上的F点处,将△ACH沿着CH对折,使点A落在OC上的G点处。
(1)求证:四边形OECH是平行四边形;
(2)当点B运动到使得点F,G重合时,求点B的坐标,并判断四边形OECH是什么四边形?说明理由;
(3)当点B运动到使得点F,G将对角线OC三等分时,求点B的坐标。




 ,正确的结果是( )
,正确的结果是( )







 和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。
和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号