初中数学统计量的选择解答题

从全校1200名学生中随机选取一部分学生进行调查，调查情况：A：上网时间小时；B：1小时＜上网时间小时；C：4小时＜上网时间小时；D：上网时间＞7小时．统计结果制成了如图统计图：

（1）参加调查的学生有      人；
（2）请将条形统计图补全；
（3）请估计全校上网不超过7小时的学生人数．

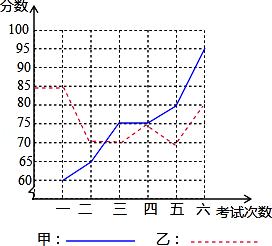
甲、乙两名同学进入初三后，某科6次考试成绩如图：
（1）请根据下图填写如表：

	平均数	方差	中位数	众数	极差
甲	75		75
乙		33．3			15

 
（2）请你分别从以下两个不同的方面对甲、乙两名同学6次考试成绩进行分析：
①从平均数和方差相结合看；
②从折线图上两名同学分数的走势上看，你认为反映出什么问题？

在“有效学习儒家文化”活动中，甲、乙两校师生共150人进行了汇报演出，小林将甲、乙两校参加各项演出的人数绘制成如下不完整的统计图表，根据提供的信息解答下列问题：
甲校参加汇报演出的师生人数统计表

	百分比	人数
话剧	50%	m
演讲	12%	6
其他	n	19

（1）m=      ，n=      ；
（2）计算乙校的扇形统计图中“话剧”的圆心角度数；
（3）哪个学校参加“话剧”的师生人数多？说明理由．

从全校1200名学生中随机选取一部分学生进行调查，调查情况：A：上网时间小时；B：1小时＜上网时间小时；C：4小时＜上网时间小时；D：上网时间＞7小时．统计结果制成了如
图统计图：

（1）参加调查的学生有  人；
（2）请将条形统计图补全；
（3）请估计全校上网不超过7小时的学生人数．

某校准备选出甲、乙两人中的一人参加县里的射击比赛，他们在相同条件下各射靶5次，成绩统计如下：

命中环数/环	7	8	9	10
甲命中的频数/次	1	1	0	3
乙命中的频数/次	0	1	3	1

 
（1）求甲、乙两人射击成绩的方差分别是多少？
（2）已知该校选手前三年都取得了县射击比赛的第一名，请问应选择谁去参加比赛？

下面图①、图②是某校调查部分学生是否知道母亲生日情况的扇形和条形统计图：

根据上图信息，解答下列问题：
（1）本次共调查了      名学生，扇形统计图中“知道”所占的百分数是         ，并补全条形统计图；
（2）若全校共有3000名学生，请你估计这所学校有多少名学生知道母亲的生日？

某校同学参加语文知识竞赛，将学生的成绩，进行整理后分成5组，绘制成频数分布直方图如下，图中从左到右各小组的频率分别是0．0625，0．25，0．375，0．1875，0．125且已知最右边小组的频数为6，结合直方图提供的信息，解答下列问题：

（1）该校参加语文知识竞赛学生共有多少人？
（2）成绩落在哪组数据范围内的人数最多？是多少？
（3）求成绩在80分以下的学生人数．

为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

（1）活动启动之初学生“一周诗词诵背数量”的中位数为　　；

（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

（3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

下表给出了某班6名同学身高情况（单位：cm）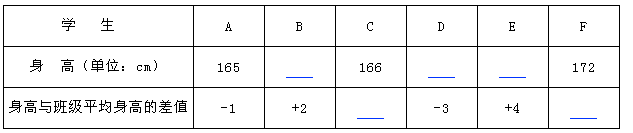

（1）完成表中空的部分；
（2）他们6人中最高身高比最矮身高高多少？
（3）如果身高达到或超过平均身高时叫达标身高，那么这6个同学身高的达标率是多少？（精确到小数点后两位）

今年3月5日，我校组织全体学生参加了“走出校门，服务社会”的活动．九年级三班同学统计了该天本班学生打扫街道，去敬老院服务和到社区文艺演出的人数，并做了如下直方图和扇形统计图．请根据同学所作的两个图形．解答：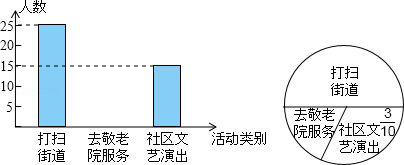

（1）九年级三班有多少名学生；
（2）补全直方图的空缺部分；
（3）若九年级有800名学生，估计该年级去敬老院的人数．

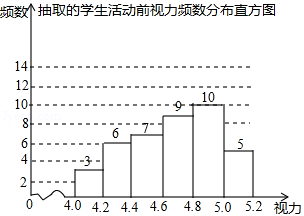
为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到 $0.1)$；活动后，再次检查这部分学生的视力，结果如表所示．

分组	频数
$4.0⩽x<4.2$	2
$4.2⩽x<4.4$	3
$4.4⩽x<4.6$	5
$4.6⩽x<4.8$	8
$4.8⩽x<5.0$	17
$5.0⩽x<5.2$	5

（1）求所抽取的学生人数；

（2）若视力达到4.8及以上为达标，估计活动前该校学生的视力达标率；

（3）请选择适当的统计量，从两个不同的角度分析活动前后相关数据，并评价视力保健活动的效果．

一次期中考试中，甲、乙、丙、丁、戊五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）

	甲	乙	丙	丁	戊	平均分	标准差
数学	71	72	69	68	70
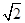英语	88	82	94	85	76	85

 
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式：
标准分=（个人成绩一平均成绩）÷成绩标准差．
从标准分看，标准分大的考试成绩更好，请问甲同学在本次考试中，数学与英语哪个学科考得更好？

君畅中学计划购买一些文具送给学生，为此学校决定围绕“在笔袋、圆规、直尺、钢笔四种文具中，你最需要的文具是什么？（必选且只选一种）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据以上信息回答下列问题：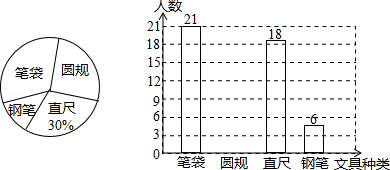

（1）在这次调查中，最需要圆规的学生有多少名？并补全条形统计图；
（2）如果全校有970名学生，请你估计全校学生中最需要钢笔的学生有多少名？

我市教育行政部门为了了解七年级学生每学期参加综合实践活动的情况，随机抽样调查了实验中学七年级学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）．

请你根据图中提供的信息，回答下列问题：
（1）求出扇形统计图中a的值，并求出该校七年级学生总数；
（2）分别求出活动时间为5天、7天的学生人数，并补全频数分布直方图；
（3）如果我市共有七年级学生6000人，请你估计“活动时间不少于4天”的大约有多少人？

某校为了解学生对三种国庆活动方案的意见，对该校学生进行了一次抽样调查（被调查学生至多赞成其中的一种方案），现将调查结果绘制成如图两幅不完整的统计图．请根据图中提供的信息解答下列问题

（1）这次共调查了多少名学生？扇形统计图中方案1所对应的圆心角的度数为多少度？
（2）请把条形统计图补充完整；
（3）已知该校有1000名学生，试估计该校赞成方案1的学生约有多少人？