北京市大兴区八年级下学期期末考试数学试卷

方程：x（x+1）=3（x+1）的解的情况是（　　）

已知等腰梯形的两底之差等于腰长，则腰与下底的夹角为（　　）

将方程x²+4x+1=0配方后，原方程变形为（　　）

A．	B．
C．	D．

某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下：

对这两名运动员的成绩进行比较，下列四个结论中，不正确的是（　　）

下列命题中，真命题是（　　）

若一元二次方程x²+2x+m=0有实数解，则m的取值范围是（　　）

A．

B．

C．

D．

为了了解某校九年级学生的体能情况，随机抽查了其中50名学生，测试1分钟仰卧起坐的成绩（次数），进行整理后绘制成如图所示的频数分布直方图（注：15～20包括15，不包括20，以下同），请根据统计图计算成绩在20～30次的频率是（　　）

梯形的上底长为6cm，过上底一个顶点引一腰的平行线，交下底所得的三角形的周长是19cm，那么这个梯形的周长等于（　　）

一件商品的原价是100元，经过两次提价后的价格为121元．如果每次提价的百分率都是x，根据题意，下面列出的方程正确的是（　　）

A．	B．
C．	D．

一个多边形有9条对角线，则这个多边形有多少条边（　　）

若x=2是关于x的方程x²﹣x﹣a²+5=0的一个根，则a的值为　  　．

如果关于x的一元二次方程x²﹣6x+c=0（c是常数）没有实根，那么c的取值范围是　  　．

将两个形状相同的三角板放置在一张矩形纸片上，按图示画线得到四边形ABCD，则四边形ABCD的形状是　   　．

已知关于x的一元二次方程的一个根是1，写出一个符合条件的方程：　        　．

如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m．若矩形的面积为4m²，则AB的长度是　 　m（可利用的围墙长度超过6m）．

一组数据3、4、5、a、7的平均数是5，则它的方差是　 　．

阅读材料：设一元二次方程ax²+bx+c=0（a≠0）的两根为x₁，x₂，则两根与方程系数之间有如下关系：x₁+x₂=﹣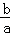，x₁•x₂=．
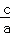根据该材料填空：已知x₁，x₂是方程x²+6x+3=0的两实数根，则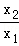+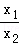的值为　  　．

如图，在梯形ABCD中，AD∥BC，AD=4，BC=12，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当运动时间为　2或　秒时，以点P，Q，E，D为顶点的四边形是平行四边形．

解方程：（2x+3）²﹣2x﹣3=0．

用配方法解方程：2x²+1=3x．

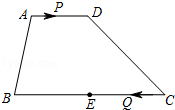
（根据市教委提出的学生每天体育锻炼不少于1小时的要求，为确保阳光体育运动时间得到落实，某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查，其中部分结果记录如下：

 
请你将频数分布表和频数分布直方图补充完整．

己知一元二次方程x²﹣3x+m﹣1=0．
（1）若方程有两个不相等的实数根，求实数m的取值范围；
（2）若方程有两个相等的实数根，求此时方程的根．

如图，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的小正方形，使得留下的图形（图中阴影部分）面积是原矩形面积的80%，求所截去小正方形的边长．

如图，在梯形ABCD中，DC∥AB，AD=BC，BD平分∠ABC，∠A=60°．过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF，求证：△DEF为等边三角形．

阅读理解：
方程ax²+bx+c=0（a≠0）的根是x=．
方程y²+by+ac=0的根是y=．
因此，要求ax²+bx+c=0（a≠0）的根，只要求出方程y²+by+ac=0的根，再除以a就可以了．
举例：解方程72x²+8x+=0．
解：先解方程y²+8y+72×=0，得y₁=﹣2，y₂=﹣6．
∴方程72x²+8x+=0的两根是x₁=，x₂=．
即x₁=﹣，x₂=﹣．
请按上述阅读理解中所提供的方法解方程49x²+6x﹣=0．