如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD
(1)求证:∠CDE=2∠B
(2)若BD:AB= :2,求⊙O的半径及弦DF的长
:2,求⊙O的半径及弦DF的长
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,矩形DEFG的顶点G与△ABC的顶点C重合,边GD、GF分别与AC,BC重合。GD=12,GF=16,矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动,点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点H,矩形DEFG、点Q同时出发,当点Q到达点A时停止运动,矩形DEFG也随之停止运动。设矩形DEFG、点Q运动的时间是t秒(t>0)。(1)求线段DF的长;
(2)求运动过程中,矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式(写出自变量的取值范围);
(3)射线QK能否把矩形DEFG分成面积相等的两部分?若能,求出t值,若不能,说明理由;
(4)连接DH,当DH∥AB时,请直接写出t值。
如图,矩形OABC中,A(6,0)、C(0,2 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
(1)①点B的坐标是 ;②∠CAO= 度;③当点Q与点A重合时,点P的坐标为 ;(直接写出答案)
(2)设OA的中心为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.
(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.
如图所示,当小华站立在镜子 前
前 处时,他看自己的脚在镜中的像的俯角为
处时,他看自己的脚在镜中的像的俯角为 ;如果小华向后退0.5米到
;如果小华向后退0.5米到 处,这时他看自己的脚在镜中的像的俯角为
处,这时他看自己的脚在镜中的像的俯角为 .求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据: )
)
如图,在直角坐标系中,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
(1)点P在运动过程中, ∠CPB= ;
∠CPB= ;
(2)当m=3时,试求矩形CEGF的面积;
(3)当P在运动过程中,探索 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
(4)如果点P在射线AB上运动,当△PDE的面积为4时,请你求出CD的长度
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作: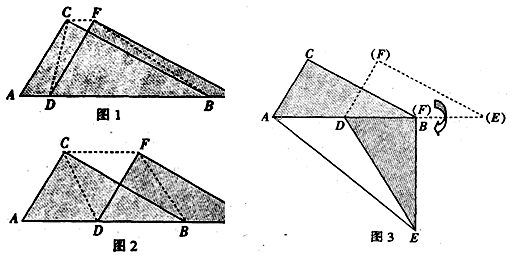
(1)如图1,△DEF沿线段AB向右平移(即D点在线段AB内移动) ,连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,四边形CDBF面积为 _______;
(2)如图2,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)如图3,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sin∠AED的值.
如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长.(参考数据:=1.73)
某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).
请求出旗杆MN的高度.(参考数据: ≈1.4,
≈1.4, ≈1.7,结果保留整数。)
≈1.7,结果保留整数。)
如图,△ABC中,AB=4,BC=3,AC=5. 以AB所在直线为轴旋转一周形成的几何体的侧面积为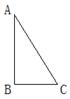
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上。点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
(1) 当t = 2时,tan∠NAO = ▲ ;
(2) 在直角坐标系中,取定点P(3,8),则在点M运动过程中,当以M、N、C、P为顶点的四
边形是梯形时,点M的坐标为 ▲ .
如图,边长为 的正方形ABCD沿直线
的正方形ABCD沿直线 向右滚动.当正方形滚动一周时,正方形中心O经过的路程为 此时点A经过的路程为 ;
向右滚动.当正方形滚动一周时,正方形中心O经过的路程为 此时点A经过的路程为 ;
(本题满分11分)
如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;(2分)
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3分)
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.(4分)
