[浙江]2011-2012年浙江省萧山城区九年级12月月考数学卷
下列命题中,是真命题的为
| A.三个点确定一个圆 |
| B.一个圆中可以有无数条弦,但只有一条直径 |
| C.圆既是轴对称图形,又是中心对称图形 |
| D.同弧所对的圆周角与圆心角相等 |
已知二次函数y=a(x-1)2+b有最小值-1, 则a,b的大小关系为
| A.a>b | B.a=b | C.a<b | D.大小不能确定 |
在比例尺为 的地图上,某建筑物在图上的面积为50 cm2,则该建筑物实际占地面积为
的地图上,某建筑物在图上的面积为50 cm2,则该建筑物实际占地面积为
| A.50 m2 | B.5000 m2 | C.50000 m2 | D.500000 m2 |
下列关于相似的说法:①所有的等腰直角三角形一定相似;②所有的菱形一定相似;③所有的全等三角形一定相似;④所有的有一个角为60°的等腰梯形一定相似.其中说法正确的有
| A.1个 | B.4个 | C.3个 | D.2个 |
如图,梯形ABCD中,AB∥DC,AB⊥BC,AB=2cm,CD=4cm.以BC上一点O为圆心的圆经过A、D两点,且∠AOD=90°,则圆心O到弦AD的距离是
A. cm cm |
B. cm cm |
C. cm cm |
D. cm cm |
如图,AC是⊙O的直径,BD是⊙O的弦,EC∥AB交⊙O于E,则图中与 ∠BOC相等的角共有
∠BOC相等的角共有
| A.2个 | B.3个 | C.4个 | D.5个 |
如图,AC、BC是两个半圆的直径,∠ACP=30°,若AB=10cm,则PQ的值为
A.5cm B. C.6 D.8cm
C.6 D.8cm
若二次函数 的顶点在第一象限,且经过点(0,1)、(-1,0),则Y
的顶点在第一象限,且经过点(0,1)、(-1,0),则Y 的取值范围是
的取值范围是
| A.Y>1 | B.-1<Y<1 | C.0<Y<2 | D.1<Y<2 |
二次函数y=ax2+bx+c的图象与x轴相交于(-1, 0)和(5, 0)两点,则该抛物线的对称轴是 .
如图,在△ABC中,EF∥BC,AE=2BE,则△AEF与梯形BCFE的面积比为________.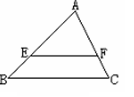
如图,A、B是双曲线 的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是____ _____。
的一个分支上的两点,且点B(a,b)在点A的右侧,则b的取值范围是____ _____。
如图,边长为 的正方形ABCD沿直线
的正方形ABCD沿直线 向右滚动.当正方形滚动一周时,正方形中心O经过的路程为 此时点A经过的路程为 ;
向右滚动.当正方形滚动一周时,正方形中心O经过的路程为 此时点A经过的路程为 ;
已知双曲线 与直线
与直线 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线 于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为 .
如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm/秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间.
如图(1),某建筑物有一抛物线形的大门,小强想知道这道门的高度.他先测出门的宽度 ,然后用一根长为
,然后用一根长为 的小竹杆
的小竹杆 竖直地接触地面和门的内壁,并测得
竖直地接触地面和门的内壁,并测得 .小强画出了如图(2)的草图,请你帮他算一算门的高度
.小强画出了如图(2)的草图,请你帮他算一算门的高度 有多少米。(保留2个有效数字).
有多少米。(保留2个有效数字).
在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数 的图象交于A(1,4)、B(3,m)两点。
的图象交于A(1,4)、B(3,m)两点。(1)求一次函数的解析式;
(2)求△AOB的面积。
(3)当
 取何值时,反比例函数的值大于一次函数的值.(直接写出答案)
取何值时,反比例函数的值大于一次函数的值.(直接写出答案)
有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。(1)设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;(2)若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为 元,试写出
元,试写出 与
与 之间的函数关系式;
之间的函数关系式;(3)李经理将这批野生菌存放多少天后出售可获得最大利润
 元?(利润=销售总额-收购成本-各种费用)
元?(利润=销售总额-收购成本-各种费用)
如图,在半径是2的⊙O中,点Q为优弧 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在 上有一动点P,且点P到弦MN所在直线的距离
上有一动点P,且点P到弦MN所在直线的距离 。
。
(1)求弦MN的长;
(2)试求阴影部分面积
 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)试分析比较,当自变量
 为何值时,阴影部分面积
为何值时,阴影部分面积 与
与 的大小关系。
的大小关系。
已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.(1)求A、B、C三点的坐标;
(2)求此抛物线的表达式;
(3)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(4)在(3)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由.

 ,则
,则 等于
等于





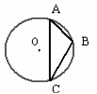
 ,求侧面展开后所得扇形的圆心角的度数。
,求侧面展开后所得扇形的圆心角的度数。 粤公网安备 44130202000953号
粤公网安备 44130202000953号