如图,在半径是2的⊙O中,点Q为优弧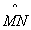 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在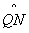 上有一动点P,且点P到弦MN所在直线的距离
上有一动点P,且点P到弦MN所在直线的距离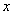 。
。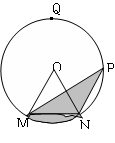
(1)求弦MN的长;
(2)试求阴影部分面积
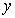 与
与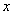 的函数关系式,并写出自变量
的函数关系式,并写出自变量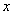 的取值范围;
的取值范围;(3)试分析比较,当自变量
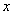 为何值时,阴影部分面积
为何值时,阴影部分面积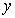 与
与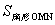 的大小关系。
的大小关系。
相关知识点
推荐套卷
如图,在半径是2的⊙O中,点Q为优弧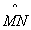 的中点,圆心角∠MON=60°,在
的中点,圆心角∠MON=60°,在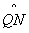 上有一动点P,且点P到弦MN所在直线的距离
上有一动点P,且点P到弦MN所在直线的距离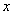 。
。
(1)求弦MN的长;
(2)试求阴影部分面积
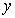 与
与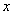 的函数关系式,并写出自变量
的函数关系式,并写出自变量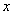 的取值范围;
的取值范围;(3)试分析比较,当自变量
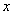 为何值时,阴影部分面积
为何值时,阴影部分面积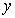 与
与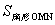 的大小关系。
的大小关系。