[浙江]2012届浙江省温州地区初三适应性考试数学卷
.某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数是
A.9.4×10-7 m B.9.4×107m C.9.4×10-8m D.9.4×108m
2012年4月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35 ,31 ,33,30 ,33 ,31,则下列表述错误的是
| A.众数是31 | B.中位数是30 | C.平均数是32 | D.极差是5 |
如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67º,则∠1=

| A.23º | B.46º | C.67º | D.78º |
已知二次函数 ,则
,则
| A.其图象的开口向上 | B.其图象的对称轴为直线 |
| C.其最大值为4 | D.当 时, 时, 随 随 的增大而减少 的增大而减少 |
围棋盒子中有 颗白色棋子和
颗白色棋子和 颗黑色棋子,从盒子中随机取出一颗棋子,取得白色棋子的概率是
颗黑色棋子,从盒子中随机取出一颗棋子,取得白色棋子的概率是 .如果在原有的棋子中再放进4颗黑色棋子,此时从盒子中随机取出一颗棋子为白色棋子的概率是
.如果在原有的棋子中再放进4颗黑色棋子,此时从盒子中随机取出一颗棋子为白色棋子的概率是 ,则原来盒子中有白色棋子
,则原来盒子中有白色棋子
| A.4颗 | B.6颗 | C.8颗 | D.12颗 |
如图,在等腰梯形ABCD中, ,点E、F分别是AD、AB的中点,且
,点E、F分别是AD、AB的中点,且 ,若AD=5,EF=6,则CF的长为
,若AD=5,EF=6,则CF的长为
| A.6.5 | B.6 | C.5 | D.4 |
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
 ;
;  DO∥AB
DO∥AB CD=AD;
CD=AD; △BDE∽△BCD;
△BDE∽△BCD; 

正确的有
| A.①② | B.①④⑤ | C.①②④⑤ | D.①②③④⑤ |
表一给出了正比例函数y1=kx的图象上部分点的坐标,表二给出了反比例函数 2=
2= 的图象上部分点的坐标,则当y1= y2时,x的值为 ▲ ;
的图象上部分点的坐标,则当y1= y2时,x的值为 ▲ ;
表一 表二
| x |
0 |
1 |
2 |
3 |
| y1 |
0 |
3 |
6 |
9 |
| x |
0.5 |
1 |
2 |
4 |
| y2 |
6 |
3 |
1.5 |
0.75 |
矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕AE上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为 ▲ ;
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上。点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
(1) 当t = 2时,tan∠NAO = ▲ ;
(2) 在直角坐标系中,取定点P(3,8),则在点M运动过程中,当以M、N、C、P为顶点的四
边形是梯形时,点M的坐标为 ▲ .
(本题6分)在下列四个条件中:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.请
选出两个作为条件,得出△AED是等腰三角形(写出一个即可),并加以证明.
已知: ▲ ;
求证:△AED是等腰三角形.
证明:
(本题6分)如图所示,小杨在处州公园的A处正面观测电子屏幕,测得屏幕上端C处的仰角为27º,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45º.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果精确到0.1m,参考数据: ≈1.41,sin27°≈0.45 ,cos27°≈0.89 ,tan27°≈0.51).
≈1.41,sin27°≈0.45 ,cos27°≈0.89 ,tan27°≈0.51).
2012年5月13日为母亲节,某校结合学生实际,开展了形式多样的感恩教育活动.下面图1,图2分别是该校调查部分学生是否知道母亲生日情况的扇形统计图和频数分布直方图.
根据上图信息,解答下列问题:
(1)被调查的学生中,记不清母亲生日情况的学生有 ▲ 人;
(2)本次被调查的学生总人数有 ▲ ,并补全频数分布直方图2;
(3)若这所学校共有学生2400人,已知被调查的学生中,知道母亲生日的女生人数是男生人数的2倍,请你通过计算估计该校知道母亲生日的女生和男生分别有多少人?
如图,过点B(2,0)的直线l: 交y轴于点A,与反比例函数
交y轴于点A,与反比例函数 的图象交于点C(3,n).、
的图象交于点C(3,n).、
(1)求反比例函数的解析式;
(2)将△OBC绕点O逆时针方向旋转α角(α为锐角),
得到△OB′C′.当OC′⊥AB时,求点C运动的路径长.
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD 3,AC=3
3,AC=3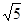 ,求⊙O的半径长.
,求⊙O的半径长.
△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB =  ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
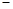 2) 的结果是
2) 的结果是
 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是
 ▲ ;
▲ ; 
 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB =" 2OC=" 3.
 DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式; 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号