△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 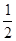 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究: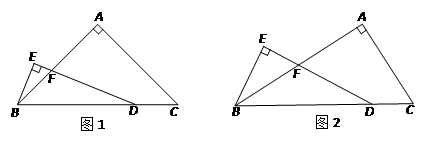
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.
相关知识点
推荐套卷
△ABC中,∠A=90°,点D在线段BC上(端点B除外),∠EDB = 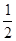 ∠C,BE⊥DE于点E,DE与AB相交于点F.
∠C,BE⊥DE于点E,DE与AB相交于点F.
(1)当AB = AC时(如图1)
①∠EBF= ▲ °;
②小明在探究过程中发现,线段FD 与BE始终保持一种特殊的数量关系,请你猜想这个关系,并利用所学知识证明猜想的正确性;
(2)探究:
当AB = kAC时(k>0,如图2),用含k的式子表示线段FD与BE之间的数量关系,请直接写出结果.