 如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于
如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于
| A.3:2 | B.3:1 | C.1:1 | D.1:2 |
如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若 ,
, ,
,
则 的值为( )
的值为( )

A. |
B. |
C. |
D. |
如图,在△ABC中,AD,BE是两条中线,则S△EDC∶S△ABC =( )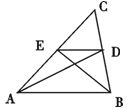
| A.1∶2 | B.1∶4 | C.1∶3 | D.2∶3 |
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )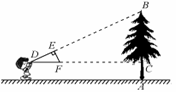
| A.12m | B.13.5m | C.15m | D.16.5m |
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为
后得到线段CD,则端点C的坐标为
| A.(3,3) | B.(4,3) | C.(3,1) | D.(4,1) |
如图,小明作出了边长为1的第1个正△A1B1C1,算出了正△A1B1C1的面积.然后分别取△A1B1C1三边的中点A2、B2、C2,作出了第2个正△A2B2C2,算出了正△A2B2C2的面积.用同样的方法,作出了第3个正△A3B3C3,算出了正△A3B3C3的面积…,由此可得,第10个正△A10B10C10的面积是( )

A. |
B. |
C. |
D. |
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( ).
A.△AED≌△AEF B.△ABE∽△ACD
C.BE+DC>DE D.BE2+DC2=DE2
将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )

A. |
B. |
C. 或4 或4 |
D. 或4 或4 |
如图, 为半圆
为半圆 的直径,
的直径, 、
、 分别切⊙
分别切⊙ 于
于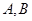 两点,
两点, 切⊙
切⊙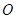 于点
于点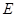 ,
, 与
与 相交于
相交于 ,
, 与
与 相交于
相交于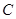 ,连结
,连结 、
、 、
、 ,对于下列结论:①
,对于下列结论:① ;②
;② ;③
;③ ;④
;④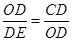 .
.
其中结论正确的个数是( ).
A. |
B. |
C. |
D. |
如图,△ABC中,∠B=90°,AB=5,BC=12,将△ABC沿DE折叠,使点C落在AB边上的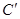 处,并且
处,并且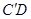 ∥BC,则CD的长是( ).
∥BC,则CD的长是( ).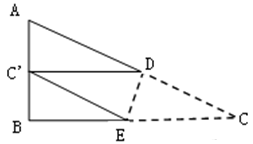
A.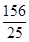 |
B.6 | C.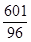 |
D.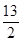 |
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若 ,AD
,AD 9,则AB等于( )
9,则AB等于( )
A.10 B.11 C.12 D.16
如图,在等边△ 中,
中, ,当直角三角板
,当直角三角板 的
的 角的顶点
角的顶点 在
在 上移动时,斜边
上移动时,斜边 始终经过
始终经过 边的中点
边的中点 ,设直角三角板的另一直角边
,设直角三角板的另一直角边 与
与 相交于点E.设
相交于点E.设 ,
, ,那么
,那么 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )

如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
| A.3:2 | B.3:1 | C.1:1 | D.1:2 |