山东省陵县九年级学业水平考试数学试卷
将一直角三角板与两边平行的纸条如图1放置.已知∠1=30°,则∠2的度数为( )
| A.30° | B.45° | C.50° | D.60° |
下列命题中,不是真命题的是( )
| A.掷一枚均匀的骰子,骰子停止转动后6点朝上是必然事件 |
| B.了解一批电视机的使用寿命,适合用抽样调查的方式. |
| C.若a为实数,则|a|<0是不可能事件 |
D.甲、乙两人各进行10次射击,两人射击成绩的方差分别为 =2, =2,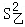 =4,则甲的射击成绩更稳定 =4,则甲的射击成绩更稳定 |
当kb<0时,一次函数y=kx+b的图象一定经过( )
| A.第一、三象限 | B.第一、四象限 |
| C.第二、三象限 | D.第二、四象限 |
已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
| A.a是无理数 | B.a是方程x2﹣8=0的解 |
| C.a是8的算术平方根 | D.a满足不等式组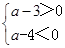 |
如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x
轴正方向平移,使⊙P与y轴相切,则平移的距离为( )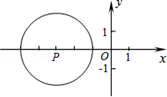
| A.1 | B.1或5 | C.3 | D.5 |
如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
| A.3:2 | B.3:1 | C.1:1 | D.1:2 |
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A. |
B. |
C.4 | D.5 |
若函数y=mx2+(m+2)x+ m+1的图象与x轴只有一个交点,那么m的值为( )
m+1的图象与x轴只有一个交点,那么m的值为( )
| A.0 | B.0或2 | C.2或﹣2 | D.0,2或﹣2 |
某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图5的折线统计图,则符合这一结果的实验最有可能的是( )
| A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” |
| B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 |
| C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球 |
| D.掷一个质地均匀的正六面体骰子,向上的面点数是4 |
如图6,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y= (k≠0)中k的值的变化情况是( )
| A.一直增大 | B.一直减小 | C.先增大后减小 | D.先减小后增大 |
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
| x |
﹣1 |
0 |
1 |
3 |
| y |
﹣1 |
3 |
5 |
3 |
下列结论:
(1)ac<0; (2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
如果从一卷粗细均匀的电线上截取1米长的电线,称得它的质量为a克,再称得剩余电线的质量为b克,那么原来这卷电线的总长度是 米.
如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀,从中随机抽取两张卡片,这两张卡片上的算式只有一个正确的概率是 .
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为 .
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN= 
如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
区教育局为了解我区八年级学生参加社会实践活动情况,随机抽查了某校部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)
请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该校共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
如图,直线y=mx与双曲线y= 相交于A、B两点,A点的坐标为(1,2)
相交于A、B两点,A点的坐标为(1,2)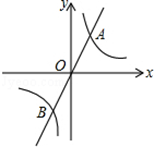
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx> 时,x的取值范围;
时,x的取值范围;
(3)计算线段AB的长.
山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
| |
A型车 |
B型车 |
| 进货价格(元) |
1100 |
1400 |
| 销售价格(元) |
今年的销售价格 |
2000 |
请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
习题如图13(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°﹣45°=45°=∠EAF,
又∵AE′=AE,AF=AF
∴△AE′F≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究
观察分析:观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;④∠EAF= ∠BAD.
∠BAD.
类比猜想:(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
研究一个问题,常从特例入手,请同学们研究:如图13(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF= ∠BAD时,EF=BE+DF吗?
∠BAD时,EF=BE+DF吗?
归纳概括:反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题: .
 的立方根是( )
的立方根是( ) +
+ ,x2=
,x2=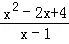 +2﹣x)÷
+2﹣x)÷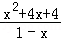 ,其中x满足x2﹣4x+3=0.
,其中x满足x2﹣4x+3=0.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号