如图,设抛物线C1: , C2:
, C2: ,C1与C2的交点为A,
,C1与C2的交点为A,
B,点A的坐标是 ,点B的横坐标是-2.
,点B的横坐标是-2.
(1)求 的值及点B的坐标;
的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,在DH的右侧作正三角形DHG. 过C2顶点M的直线记为 ,且
,且 与x轴交于点N.
与x轴交于点N.
①若 过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
过△DHG的顶点G,点D的坐标为(1, 2),求点N的横坐标;
②若 与△DHG的边DG相交,求点N的横坐标的取值范围.
与△DHG的边DG相交,求点N的横坐标的取值范围.
等腰△ABC,AB=AC=8,∠BAC=120°,P为BC的中点,小亮拿着300角的透明三角板,使300角的顶点落在点P,三角板绕P点旋转.
(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
①探究1:△BPE与△CFP还相似吗?
②探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
③设EF=m,△EPF的面积为S,试用m的代数式表示S.


如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D.若CD=CF,则 .
. 
梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10).
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1 = 0.5m,最下面一级踏板的长度A7B7 = 0.8m.则第五级踏板A5B5的长度为 ( )
| A.0.6m | B.0.65m | C.0.7m | D.0.75m |
已知:如图,在梯形ABCD中,AD∥BC,∠DCB = 90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
(1)当P点在BC边上运动时,求证:△BOP∽△DOE;
(2)设(1)中的相似比为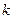 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
①当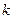 = 1时,是 ;
= 1时,是 ;
②当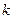 = 2时,是 ;
= 2时,是 ;
③当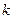 = 3时,是 .
= 3时,是 .
请证明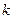 = 2时的结论.
= 2时的结论.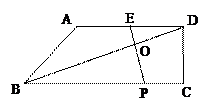

(本题14分)如图11,在△ABC中,∠ACB= ,AC=BC=2,M是边AC的中点,
,AC=BC=2,M是边AC的中点,
CH⊥BM于H.
(1)试求sin∠MCH的值;
(2)求证:∠ABM=∠CAH;
(3)若D是边AB上的点,且使△AHD为等腰三角形,请直接写出AD的长为________.
观察右图,在下列四种图形变换中,该图案不包含的变换是【 】
| A.平移 | B.轴对称 | C.旋转 | D.位似 |
如图9是置于水平地面上的一个球形储油罐,小敏想测量它的半径.在阳光下,他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(即AB=10米);同一时刻,他又测得竖直立在地面上长为1米的竹竿的影子长为2米,则球的半径是_ 米.
(11·天水)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做
了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜
子放在离树(AB)8.7m的点E处,然后观测考沿着直线BE后退到点D,这时恰好在镜子里
看到树梢顶点A,再用皮尺量得DE=2.7m,观测者目高CD=1.6m,则树高AB约是_
▲ .(精确到0.1m)
如图,在边长为8的正方形ABCD
中,点O为AD上一动点(4<OA<8),以O为圆心 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1) 求证:△ODM∽△MCN;
(2) 设DM=x,求OA的长(用含x的代数式表示);
(3) 在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
(本小题满分8分)如图10,在6×8的网格图中,每个小正方形边长均为1,点
O和△ABC的顶点均为小正方形的顶点.
⑴以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2
⑵连接⑴中的AA′,求四边形AA′C′C的周长.(结果保留根号)
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥A B,EF∥AC,
B,EF∥AC,
得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边
形E1D1FF1,它的面积记作S2.照此规律作下去,则S2011= .
如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则的 值为( )
值为( )
A. |
B. |
C. |
D. |